Ex twee MA funktsioon. Kasvav ja kahanev funktsioon intervalliga, äärmuslikud. Tuletisinstrument ja selle roll
Emmevälja funktsiooni funktsioon on funktsiooni määratluse ala punkt, kus funktsiooni väärtus on minimaalne või maksimaalne väärtus. Funktsiooni väärtused nendes punktides nimetatakse äärmuslikuks (minimaalsed ja maksimaalsed) funktsioonid.
Määratlus. Punkt x.1 Funktsioonide määratluspiirkonnad f.(x.) Kutsus maksimaalse funktsiooni punkt Kui funktsioon funktsioon selles küsimuses on rohkem funktsioone funktsioone üsna lähedal IT punktid asuvad paremal ja vasakul (see tähendab, et ebavõrdsus toimub f.(x.0 ) > f.(x.0 + Δ x.) x.1 Maksimaalne.
Määratlus. Punkt x.2 Funktsioonide määratluspiirkonnad f.(x.) Kutsus minimaalse funktsiooni punktKui selle funktsiooni väärtus selles küsimuses on väiksem kui funktsiooni väärtused üsna lähedal IT-punktide jaoks, mis asuvad paremal ja vasakul (st ebavõrdsus) f.(x.0 ) < f.(x.0 + Δ x.) ). Sel juhul öeldakse, et funktsioon on hetkel x.2 minimaalne.
Oletame x.1 - Point Maksimaalne funktsioon f.(x.). Siis enne intervalli x.1 funktsioon kasvab seetõttu on tuletisinstrumentide funktsioon suurem kui null ( f. "(x.)\u003e 0) ja intervallis pärast x.1 Funktsioon väheneb seetõttu ja tuletatud funktsioon Vähem nulli ( f. "(x.) < 0 ). Тогда в точке x.1
Oletame ka seda punkti x.2 - punkt minimaalne funktsioon f.(x.). Siis enne intervalli x.2 Funktsioon väheneb ja tuletisinstrument on väiksem kui null ( f. "(x.) < 0 ), а в интервале после x.2 Funktsioon suureneb ja derivaatfunktsioon on suurem kui null ( f. "(x.)\u003e 0). Sel juhul ka punktis x.2 Tuletisinstrument on null või ei eksisteeri.
Farm Theorerem (vajalik märk ekstremi funktsiooni olemasolu). Kui punkt x.0 - Emmeväljapunkti funktsioonid f.(x.), siis sel hetkel on derivaat funktsioon null ( f. "(x.) \u003d 0) või ei eksisteeri.
Määratlus. Punktid, kus tuletisinstrumentide funktsioon on null või ei ole olemas kriitilised punktid .

Näide 1. Mõtle funktsiooni.
Punktis x. \u003d 0 derivaatfunktsioon võrdne nulliga, seega punkt x. \u003d 0 on kriitiline punkt. Siiski, nagu on näha funktsiooni graafikus, suureneb see kogu määratluse valdkonnas, nii et punkt x. \u003d 0 ei ole selle funktsiooni äärmuslik punkt.
Seega on tingimused, et funktsiooni tuletisinstrument on null või ei ole olemas, on vajalikud ekstremmi vajalikud tingimused, kuid mitte piisavad, kuna teiste funktsioonide näiteid võib viidata sellele, millele need tingimused teostatakse, kuid funktsioon Ei ole äärmiselt emmerdas asjakohasel punktis. seetõttu vaja on piisavalt märkeLubades hinnatakse, on äärmiselt kriitilises punktis äärmuslik ja mis on maksimaalne või minimaalne.
Teoreem (äärmusliku funktsiooni olemasolu esimene piisav tunnus). Kriitiline punkt x.0 f.(x.) Kui üleminek selle punkti kaudu muudab tuletisinstrument märgi ja kui märk muutub "pluss" kuni "miinus", siis maksimaalse punkti ja kui "miinus" "pluss", Siis minimaalne punkt.
Kui punkti lähedal x.0 Selle vasakul ja paremal pool salvestab derivaat märk, siis see tähendab, et funktsioon või ainult väheneb või ainult suureneb mõne naabruses x.0 . Sellisel juhul x.0 Äärmus ei ole.
Niisiis, funktsioonide äärmuslike punktide kindlaksmääramiseks peate tegema järgmist :
- Leia tuletisinstrument.
- Võrdsustada nulli derivaat ja määrata kriitilised punktid.
- Vaimuna või paberil märkige numbrilise telje kriitilised punktid ja määravad saadud funktsiooni märgid saadud ajavahemike järel. Kui tuletisinstrumentide märk "pluss" "miinus", kriitiline punkt on maksimaalne punkt, ja kui "miinus" "pluss", siis minimaalne punkt.
- Arvutage funktsiooni väärtuse äärmuslikes punktides.

Näide 2. Leia äärmuslikud funktsioonid ![]() .
.
Otsus. Leia tuletisinstrumentide funktsioon:
Me võrdsustame nulli derivaati kriitiliste punktide leidmiseks:
![]() .
.
Kuna iga "Iksa" väärtuste puhul ei ole nimetaja võrdne nulliga, siis võrdsustada numbrit:
Sain ühe kriitilise punkti x. \u003d 3. Määrake tuletise märk selle punktide piiritletud ajavahemike järel:
miinuse lõpmatuse intervallis kuni 3 - miinusmärk, see tähendab, et funktsioon väheneb,
vahemikus 3-st pluss lõpmatusest - märk pluss, st funktsioon suureneb.
See tähendab, punkt x. \u003d 3 on minimaalne punkt.
Leidke funktsiooni väärtus minimaalse punkti juures:
Seega leitakse funktsiooni esurm punkt: (3; 0) ja see on minimaalne punkt.
Teoreem (äärmusliku funktsiooni olemasolu teine \u200b\u200bpiisav tunnus). Kriitiline punkt x.0 on äärmuslik funktsioon f.(x.) Kui teine \u200b\u200bderivaat funktsioon selles punktis ei ole null ( f. ""(x.) ≠ 0) ja kui teine \u200b\u200bderivaat on suurem kui null ( f. ""(x.)\u003e 0), siis maksimaalne punkt ja kui teine \u200b\u200bderivaat on väiksem kui null ( f. ""(x.) < 0 ), то точкой минимума.
Märkus 1. Kui punktis x.0 Kandke null ja esimene ja teine \u200b\u200bderivaadid, siis selles küsimuses on võimatu hinnata ekstremi olemasolu teise piisava funktsiooni alusel. Sellisel juhul peate ära kasutama äärmusliku funktsiooni esimene piisav tunnusjoon.
Märkus 2. Emmevälja funktsiooni teine \u200b\u200bpiisav omadus ei ole kohaldatav ja seejärel kui esimene derivaat ei ole statsionaarses punktis (siis ei ole teist derivaati). Sellisel juhul peate nautima äärmusliku funktsiooni esimese piisava tunnuse.
Eringete funktsiooni kohalik iseloom
Esitatud määratlustest järeldub, et funktsiooni ekstrem on kohalik märk - see on funktsiooni suurim ja väikseim väärtus võrreldes järgmiste väärtustega.
Oletame, et peate oma tulu aja jooksul ühe aasta pikkusega. Kui olete teeninud 45 000 rubla mais ja 42 000 aprillis rubla ja 39.000 rubla rubla, siis mai tulu on maksimaalselt teenida funktsioone võrreldes järgmiste väärtustega. Kuid oktoobris teenisite 75 000 rubla 71 000 rubla ja 74 000 novembris rubla, nii et oktoobri kasum - minimaalsed kasumi funktsioonid võrreldes lähedalasuvate väärtustega. Ja saate hõlpsasti näha, et aprilli-mai-juuni sündmuste maksimaalne seas on väiksem kui septembris-oktoober-november.
Üldiselt rääkides võib funktsiooni intervallil mitu äärmuslikkust avaldada ja selgub, et minimaalne funktsioon on rohkem kui maksimaalne. Niisiis, mis on esitatud ülaltoodud joonisel näidatud funktsiooni jaoks.
See tähendab, et see ei tohiks arvata, et maksimaalne ja minimaalne funktsioon on vastavalt selle suurimad ja väikseimad väärtused kogu segmendis. Maksimaalse punkti puhul on funktsioon kõige olulisem ainult nende väärtustega, mida ta on kõigis punktides, üsna lähedal maksimaalse punkti ja miinimumini - väikseima väärtusega võrreldes nende väärtustega See on kõikides punktides, piisavalt lähedal minimaalsele punktile.
Seetõttu on võimalik selgitada ülaltoodud esurm-punktide kontseptsiooni ja helistage miinimumini kohalikele minimaalsetele punktidele ja maksimaalsed punktid on kohalikud maksimaalsed punktid.
Otsime Expertum Funktsioonid koos

Näide 3.
Otsus. Funktsioon on määratletud ja pidev kogu numbrilisel otsesel määral. Selle derivaat ![]() Samuti on terve numbriline otsene. Seetõttu on antud juhul ainult need, kes on kriitilised punktid. , Kust. Kriitilised punktid ja jagada kogu valdkonna funktsiooni määramise kolme monotoonsuse intervalliga :. Me valime igaüks neist ühe kontrollpunktiga ja leiame selle punkti derivaadi märk.
Samuti on terve numbriline otsene. Seetõttu on antud juhul ainult need, kes on kriitilised punktid. , Kust. Kriitilised punktid ja jagada kogu valdkonna funktsiooni määramise kolme monotoonsuse intervalliga :. Me valime igaüks neist ühe kontrollpunktiga ja leiame selle punkti derivaadi märk.
Intervall võib kontrollpunkt olla: leiame. Võttes punkti intervalli, me saame ja võttes punkti intervalli, meil on. Niisiis, intervallide ja intervalliga. Emme esimese piisava suhtumise kohaselt puudub punktis esurm (kuna tuletisinstrument salvestab märgi ajavahemikus) ja punktis on funktsioonil minimaalne (kuna ülemineku tuletis muudab selle punkti tuletist miinus pluss). Leia funktsiooni sobivad väärtused: samuti. Intervall väheneb funktsioon, sest selles intervallis ja intervalli suureneb, sest selles intervallis.
Graafi ehitamise selgitamiseks leidke ristmikupunktid koordinaatide teljega. Võrrandi saamisel on leitud juured ja st kaks punkti (0; 0) ja (4; 0) funktsiooni graafika. Kasutades kogu saadud teavet, ehitame ajakava (vt näite alguses).
Enesekatse jaoks saab arvutamisel kasutada online-kalkulaatori derivaadid .

Näide 4.Leia äärmuslike funktsioonide ja ehitada selle ajakava.
Põllu määratluspiirkond on kogu number otsene, välja arvatud punkt, st .
Uuringu vähendamiseks saate kasutada asjaolu, et see funktsioon on mõõdetav, sest  . Seetõttu on selle ajakava telje suhtes sümmeetriline Oy. Ja uuringut saab teostada ainult intervalli jaoks.
. Seetõttu on selle ajakava telje suhtes sümmeetriline Oy. Ja uuringut saab teostada ainult intervalli jaoks.
Leia derivaat ![]() ja kriitilised funktsioonid:
ja kriitilised funktsioonid:
1)  ;
;
2) ![]() ,
,
kuid funktsioon kannatab selles küsimuses lõhega, seega ei saa see olla äärmuslik punkt.
Seega on määratud funktsioonil kaks kriitilist punkti: ja. Arvestades funktsiooni valmisolekut, kontrollige teist äärmuslikku märkust ainult punktini. Selleks leidke teine \u200b\u200bderivaat ![]() Ja me määratleme oma märki, millal me saame. Kuna see on minimaalse funktsiooni punkt, samas kui
Ja me määratleme oma märki, millal me saame. Kuna see on minimaalse funktsiooni punkt, samas kui ![]() .
.
Funktsiooni funktsiooni täieliku ülevaate tegemiseks teada oma käitumist määratluse piirkonna piiride kohta:

(Siin tähistab sümbolit x. null paremale ja x. on endiselt positiivne; Samamoodi tähendab see soovi x. vasakul ja x. See jääb negatiivseks). Seega, kui siis. Järgmine, leitud
 ,
,
need. Kui siis.
Graafiku funktsioonide ristmiku punktid ei ole funktsiooni. Joonis - näite alguses.
Enesekatse jaoks saab arvutamisel kasutada online-kalkulaatori derivaadid .
Me otsime jätkuvalt äärmuslikke funktsioone koos.
Näide 8.Leia äärmuslikud funktsioonid.

Otsus. Leidke funktsiooni määratluspiirkond. Kuna peaks olema ebavõrdsus, siis me saame.
Leia esimene tuletisinstrument.
2020. juulis käivitab NASA Marsile ekspeditsiooni. Kosmoseaparaat annab elektroonilise meedia Marsile kõigi registreeritud ekspeditsiooniosaliste nimedega.
Osalejate registreerimine on avatud. Võta oma pilet selle lingi Marsi jaoks.
Kui see postitus otsustas teie probleemi või lihtsalt meeldis teile, jagage see linki oma sõpradega sotsiaalsete võrgustikega.
Üks neist koodi valikutest tuleb kopeerida ja lisada oma veebilehe koodi, eelistatavalt silte vahel
ja või kohe pärast sildi . Esimese versiooni kohaselt laaditakse Mathjax kiiremini ja aeglustab lehekülge. Kuid teine \u200b\u200bvalik jälgib automaatselt ja laadib viimaseid Mathjaxi versioone. Kui sisestate esimese koodi, tuleb seda korrapäraselt ajakohastada. Kui sisestate teise koodi, laaditakse leheküljed aeglasemalt, kuid te ei pea matšjaxi värskendusi pidevalt jälgima.Connect Matchejax on lihtsaim viis Bloggeri või WordPressi jaoks: Vidina lisamine kolmanda osapoole JavaScripti koodi sisestamiseks, et sisestada ülaltoodud allalaadimiskoodi esimene või teine \u200b\u200bversioon ja asetage vidin lähemale malli algusse (muide , see ei ole üldse vajalik, sest Mathjaxi skript on laetud asünkroonselt). See on kõik. Nüüd loe MathMl, Latex ja ASCIIMATHML Markup Syntax, ja olete valmis lisama matemaatiliste valemite veebilehtede saidi.
Teine uusaasta Eve ... Frosty Ilm ja lumehelbed akna klaasist ... Kõik see ajendas mind uuesti kirjutada ... fraktaalid ja mida ta sellest alfra kohta teab. Sel juhul on huvitav artikkel, kus on näiteid kahemõõtmelise fraktsioonistruktuuride näiteid. Siin kaalume kolmemõõtmeliste fraktsioonide keerukamaid näiteid.
Fraktaali võib selgelt ette kujutada (kirjeldada) geomeetrilise kuju või kehana (pidades silmas, et mõlemad on palju, sel juhul punktide kogum), mille üksikasjad on sama kuju ise. See tähendab, et see on iselaadne struktuur, arvestades üksikasju, mille suurenemise, näeme sama vormi kui suurendamata. Tavapärase geomeetrilise kuju (mitte fraktaalsete) puhul, suurendades näeme osad, millel on lihtsam vorm kui algne kuju. Näiteks piisavalt suure kasv, osa ellipsi näeb välja sirgjoon. Mis fraktsioonid, see ei juhtu: Mis tahes suurenemine, me jälle näeme sama keeruline kuju, mis kordab ikka ja jälle.
Benoit Mantelbrot (Benoit Mantelbrot), fraktsioonide teaduse asutaja, tema artiklis fraktsioonid ja kunst teaduse nimel kirjutas: "fraktals on geomeetrilised vormid, mis on võrdselt keerulised nende üksikasjades, nagu selle üldises vormis. See tähendab, et Kui osa fraktsioonist suurendatakse kogu suurusega, näeb välja nagu täisarv või täpselt või võimaluse korral väike deformatsiooniga. "
Väga oluline teave funktsiooni käitumise kohta annab suurendamise ja kahanemise lünki. Nende järeldus on osa protsessi uurimise funktsiooni ja ehitada ajakava. Lisaks on äärmuslikud punktid, milles on üleminek lagunemisest või suurenemisest suurenemisest, erilist tähelepanu pööratakse mõne ajavahemiku suurima ja väikseima funktsiooni väärtuse leidmisel.
Käesolevas artiklis anname vajalikud määratlused, me sõnastame piisava ülevaate funktsiooni suurendamisest ja kahanemisest intervalliga ja piisavates tingimustes ekstremmi olemasolu jaoks, kohaldame kõiki seda teooriat näidete ja ülesannete lahendamiseks.
Navigeerimine leht.
Kasvav ja kahanev funktsioon intervalliga.
Kasvava funktsiooni määratlus.
Funktsioon y \u003d f (x) suureneb intervalli x, kui iga ja ![]() Ebavõrdsus toimub. Teisisõnu, argumendi suurem väärtus vastab funktsiooni suuremale väärtusele.
Ebavõrdsus toimub. Teisisõnu, argumendi suurem väärtus vastab funktsiooni suuremale väärtusele.
Vähendamise funktsiooni määramine.
Funktsioon Y \u003d F (x) väheneb intervalli x, kui iga ![]() Ebavõrdsus toimub
Ebavõrdsus toimub ![]() . Teiste sõnadega vastab argumendi suurem väärtus funktsiooni väiksemale väärtusele.
. Teiste sõnadega vastab argumendi suurem väärtus funktsiooni väiksemale väärtusele.

Märkus: Kui funktsioon määratakse suureneva või vähendamise intervalli (A; B) otstes ja pidevalt, on see x \u003d a ja x \u003d b puhul kaasatud suurenemise või kahaneva suurenemise suurenemiseni. See ei ole vastuolus intervalli x kasvava ja kahaneva funktsiooni määratlustega.
Näiteks me teame põhiliste elementaarsete funktsioonide omadustest, mida Y \u003d SINX on määratletud ja pidev argumendi kehtivate väärtuste jaoks. Seetõttu võib sinuse funktsiooni suurenemisest intervallis väita, et segmendis kasvab.
Äärmuslikud punktid, äärmuslikud funktsioonid.
Helistama maksimaalne punkt Funktsioonid Y \u003d F (x), kui kõik X-st ebavõrdsuse ümbritsevad. Väärtus funktsiooni maksimaalse punkti nimetatakse maksimaalne funktsioon Ja tähistage.
Helistama miinimumini Funktsioonid Y \u003d F (x), kui kõik X-st ebavõrdsuse ümbritsevad. Funktsiooni väärtus miinimumi punktis nimetatakse minimaalne funktsioon Ja tähistage.
Naabruskonna punktide all mõista intervalli ![]() Kus on piisavalt väike positiivne number.
Kus on piisavalt väike positiivne number.
Minimaalsete ja maksimaalsete punktide punktid Äärmuspunktidja väärtused funktsiooni vastavad punktide esurm nimetatakse Äärmuslik funktsioon.

Ärge segage äärmusi funktsioone suurima ja väikseima funktsiooni väärtus.

Esimeses numbris saavutatakse segmendi funktsiooni suurim väärtus maksimaalsele punktile ja võrdne maksimaalse funktsiooniga ja teisel kujul - funktsiooni suurim väärtus saavutatakse punkti x \u003d b, mis ei ole maksimaalne punkt.
Piisavad tingimused suurendamise ja kahaneva funktsiooni.
Tuginedes piisavatele tingimustele (märke) suurendada ja vähendada funktsiooni on lünki kasvava ja kahaneva funktsiooni.
Siin on intervalli suurendamise ja kahaneva funktsiooni kujundamisel ajavahemikus:
- kui funktsiooni funktsioon Y \u003d F (x) derivaat on X-intervalli X-st positiivne, suureneb funktsioon x-ga;
- kui funktsiooni derivaat Y \u003d F (x) on negatiivne X-intervalli X-st negatiivne, väheneb funktsioon x-ni.
Seega, et määrata kindlaks funktsioonide suurendamise ja vähendamise lüngad:
Algoritmi selgitamiseks kaaluge funktsiooni suurendamise ja kahanemise asukoha näidet.
Näide.
Leia suurendamise ja kahaneva funktsiooni lünki.
Otsus.
Esimeses etapis peate leidma välja määratluse piirkonna. Meie näites ei tohiks nimetaja väljend selle nulliga käsitseda.
Mine leida tuletisinstrumendi funktsiooni: 
Et määrata kindlaks suurendamise ja kahanemise lüngad, mis on piisavate märkide lahendamine ebavõrdsuse lahendamine ja määratluse ala. Me kasutame intervalli meetodi üldistamist. Lumeraatori ainus kehtiv juur on X \u003d 2 ja nimetaja viitab nullile x \u003d 0 juures. Need punktid murda määratluse ala ajavahemike järel, kus tuletatud funktsioon salvestab märk. Me märgime need punktid numbrilisel liinil. Tavaliselt tähistavad plussid ja miinused, mille järel derivaat on positiivne või negatiivne. Allpool toodud noogel näitab skemaatiliselt vastava intervalli funktsiooni suurenemist või vähendamist. 
Sellel viisil,  ja
ja  .
.
Punktis x \u003d 2 funktsioon on määratletud ja pidev, nii et see tuleb lisada suurenemise kasvu suurenemise kasvu vähenemise. Punktis X \u003d 0, funktsiooni ei ole määratletud, nii et see punkt ei lülitu sisse soovitud intervallidega.
Saadud tulemuste võrdlemiseks tutvustame funktsiooni graafikut.

Vastus:
Funktsioon suureneb ![]() , intervalli vähenemine (0; 2] väheneb.
, intervalli vähenemine (0; 2] väheneb.
Piisavad esurmafunktsiooni tingimused.
MAXIMA ja MINIMA leidmiseks saate muidugi kasutada mõnda kolme märki, muidugi, kui funktsioon vastab nende tingimustele. Kõige tavalisem ja mugavam on esimene.
Esimene piisav äärmuslik seisund.
Oletame, et funktsioon Y \u003d F (x) diferentseerub selle punkti naabruses ja just punkt ise on pidev.
Teisisõnu:
Algoritm äärmuslike punktide leidmiseks äärmusliku funktsiooni esimesel märgil.
- Leidke funktsiooni määratluspiirkond.
- Leiame derivaatfunktsiooni määratluse piirkonnas.
- Määrake loendaja nullid, derivaadi derivaadi nimetaja nullid ja määratluse ala punkt, milles derivaati ei eksisteeri (kõiki loetletud punkte) võimalikud äärmuslikud punktidNende punktide läbimine võib derivaat lihtsalt oma märki muuta).
- Need punktid murda valdkonnas määrata funktsiooni funktsiooni intervallidega, kus derivaat salvestab märk. Me määrame iga intervallide derivaadi märke (näiteks derivaadi väärtuse arvutamisel eraldi intervalli mis tahes punktis).
- Me valime punkte, kus funktsioon on pidev ja läbib, mille kaudu derivaat muudab märk - nad on äärmuslikud punktid.
Liiga palju sõnu, kaaluge parimaid näiteid funktsiooni äärmuslike punktide ja funktsioonide leidmisest, kasutades äärmusliku funktsiooni esimese piisava seisundi.
Näide.
Leia äärmuslikud funktsioonid.
Otsus.
Väli määratluspiirkond on kõik kehtivad numbrid, välja arvatud X \u003d 2.
Leia derivaat: 
Nunderaatori nullid on punkte x \u003d -1 ja x \u003d 5, nimetaja viitab nullile x \u003d 2. Me tähistame neid punkte numbrilisel teljel 
Määrake derivaadi märgid iga intervalliga, selle arvutamiseks arvutame derivaadi väärtuse iga intervalli punktides, näiteks punktides x \u003d -2, x \u003d 0, x \u003d 3 ja x \u003d 6.
Järelikult on derivaat intervallile positiivne (joonisel, panna selle ajavahemiku jooksul märk). Sarnaselt 
Seetõttu paneme teise intervalli üle miinus kolmanda miinus üle neljanda pluss.
Jääb valida punkte, kus funktsioon on pidev ja selle derivaat muudab märk. Need on äärmuslikud punktid.
Punktis x \u003d -1 Funktsioon on pidev ja derivaat muudab märgi plussist miinus, seetõttu, vastavalt esimese märk Expertum, X \u003d -1 on maksimaalne punkt, see vastab maksimaalse funktsiooni  .
.
Punktis x \u003d 5 funktsioon on pidev ja derivaat muudab märgi miinus pluss, seetõttu X \u003d -1 on minimaalne punkt, see vastab minimaalse funktsiooni  .
.
Graafiline illustratsioon.

Vastus:
Pange tähele: Emme esimene piisav omadus ei nõua selle funktsiooni diferentseerimist.
Näide.
Leia äärmuslikud punktid ja äärmuslikud funktsioonid ![]() .
.
Otsus.
Väli määratluspiirkond on kõik palju kehtivaid numbreid. Funktsiooni ise saab kirjutada järgmiselt: 
Leia tuletisinstrumentide funktsioon: 
Punktis x \u003d 0 derivaati ei eksisteeri, kuna ühepoolsete piiride väärtused, kui argument on mõeldud nullini, ei lange need kokku: 
Samal ajal on esialgne funktsioon pidevalt punktis x \u003d 0 (vt sektsiooni uurimisfunktsioon järjepidevuse kohta): 
Leidke argumendi väärtused, millega derivaat muutub nulliks: 
Me märgime kõiki numbritel saadud punkte ja määrame derivaadi märgi iga intervalliga. Selleks arvutada tuletisinstrumendi väärtused iga intervalli meelevaldsetes punktides, näiteks millal x \u003d -6, x \u003d -4, x \u003d -1, x \u003d 1, x \u003d 4, x \u003d 6.
I.e, 
Seega on äärmusliku märgi esimene märk ![]() , maksimaalsed punktid on
, maksimaalsed punktid on ![]() .
.
Arvutage vastav miinimumfunktsioon 
Arvuta vastavad funktsioonid funktsiooni 
Graafiline illustratsioon.

Vastus:
 .
.
Emmevälja funktsiooni teine \u200b\u200bmärk.
Nagu näete, nõuab see äärmusliku funktsiooni funktsioon derivaadi olemasolu vähemalt teises järjekorras.
Mõtle pideva funktsiooni graafikule. y \u003d F (x)näidatud joonisel.
Tähendusfunktsioon punktis x. 1 on funktsioonide funktsiooni kõigis naaberpunktides nii vasakul kui ka paremal x. üks. Sel juhul öeldakse, et funktsioon on hetkel x. 1 maksimaalne. Punktis x. 3 funktsioonil on ilmselgelt maksimaalne. Kui arvate punkti x. 2, siis väärtustab funktsiooni väiksem kui kõik külgnevad väärtused. Sel juhul öeldakse, et funktsioon on hetkel x. 2 Minimaalne. Sarnaselt punktiga x. 4 .
Ülesanne y \u003d F (x) Punktis x. 0 on maksimaalneKui funktsiooni väärtus selles küsimuses on suurem kui selle väärtused kõigis punktides mõningase intervalliga x. 0, st. Kui selline naabruskonda on olemas x. 0 seda kõigi jaoks x.≠x. 0 , Selle naabruskonna kuulumine on ebavõrdsus f (x)<f (x. 0 ) .
Ülesanne y \u003d F (x)sellel on minimaalne Punktis x. 0 , Kui selline naabruskonda on olemas x. 0 , mis kõigile x.≠x. 0, kuuluvad sellele naabrusesse, on ebavõrdsus f (x)>f (x 0.
Punktid, kus funktsioon jõuab maksimaalse ja miinimumini nimetatakse äärmuslikeks punktideks ja funktsioonide väärtused nendes punktides on funktsiooni äärmused.
Me juhime tähelepanu asjaolule, et segmendis määratletud funktsioon võib ulatuda maksimaalse ja minimaalseks ainult vaatlusaluse segmendi sees olevate punktide juures.
Märgi, et kui funktsioon on maksimaalne punkt, see ei tähenda, et sel hetkel funktsioon on suurim väärtus kogu määratlus valdkonnas. Eespool kirjeldatud joonisel on funktsiooni funktsioon x. 1 on maksimaalne, kuigi on punkte, kus funktsiooni väärtused on suurem kui punkt x. 1 . Eriti, f.(x. 1) < f.(x. 4) s.t. Minimaalne funktsioon on suurem kui maksimaalne. Maksimaalse määratlusest tuleneb ainult sellest, et see on funktsiooni suurim väärtus punktides, maksimaalse punkti lähedal.
Teoreem 1. (ekstremmeumi olemasolu vajalik tingimus.) Kui diferentseeruv funktsioon y \u003d F (x)on punktis x \u003d x. 0 Expertum, selle derivaat selles punktis lisab nullini.
Tõendid. Olge täpselt määratleda x. 0 funktsioonil on maksimaalne. Siis piisavalt väikeste sammudega δ x. omama f (x. 0 + Δ x)
Nende ebavõrdsuse muutmine piirini δ x.→ 0 ja arvestades tuletist f. "(x. 0) eksisteerib ja järelikult ei sõltu vasakul asuv piir, kuidas δ x. → 0, saame: at δ x. → 0 – 0 f "(x. 0) ≥ 0 a δ x. → 0 + 0 f "(x. 0) ≤ 0. Alates sellest ajast f "(x. 0) määrab number, seejärel need kaks ebavõrdsust on ühiselt ainult siis, kui f "(x. 0) = 0.
Tõestatud teoreem väidab, et maksimaalsed ja minimaalsed punktid võivad olla ainult nende argumentide hulgas, kus tuletisinstrument muutub nullini.
Me pidasime juhul, kui mõne segmendi kõigis punktides funktsioon on tuletisinstrument. Kuidas juhtudel juhul, kui derivaat ei eksisteeri? Mõtle näiteid.
Näited.
- y.=|x.|.
Funktsioonil ei ole punktis derivaati x.\u003d 0 (sel hetkel graafik funktsiooni ei ole teatud puutuja), kuid sel hetkel funktsioon on minimaalne, sest y.(0) \u003d 0 ja üldse x.≠ 0y. > 0.
- Las olla x.< x
0. Siis c.< x
0 I. f "c)\u003e0.
seetõttu f "c) (x- x 0)<
0 ja seetõttu
f (x) - f (x 0 )< 0, st. f (x)< f(x 0 ).
- Las olla x\u003e X. 0. Siis c\u003e X. 0 I. f "c)< 0. Nii f "c) (x- x 0)< 0. seetõttu f (x) - f (x 0 ) <0,т.е.f (x)< f (x. 0 ) .
- Leia põllu määratluse ala f (x).
- Leia esimene tuletisinstrument f "(x).
- Määrake selle kriitilised punktid:
- leia kehtivad juured võrrandid f "(x)=0;
- leia kõik väärtused x. mille tuletisinstrumentide f "(x) ei eksisteeri.
- Kriitilise punkti vasakul ja paremal asuva derivaadi märk määrata. Kuna tuletisinstrumentide kaubamärk jääb konstantseks kahe kriitilise punkti vahel, piisab selleks, et määrata kindlaks tuletise märk mingil hetkel vasakule ja ühele punktile kriitilise punkti paremale.
- Arvutage funktsiooni väärtuse äärmuslikes punktides.
- Leia kõik funktsiooni kriitilised punktid intervallis ( a, B.) ja arvutage funktsioonide funktsioonid nendes punktides.
- Arvutage funktsiooni väärtused segmendi otstes, kui x \u003d a, x \u003d b.
- Kõigist saadud väärtustest valige suurim ja väikseim.
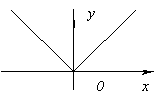
Funktsioonil ei ole derivaati x.\u003d 0, kuna see muutub lõpmatusse x.\u003d 0. Kuid sellel hetkel on funktsiooni maksimaalne.

Funktsioonil ei ole derivaati x.\u003d 0, kuna ![]() jaoks x.→ 0. Sel hetkel ei ole funktsiooni maksimaalselt minimaalselt. Tõesti, f (x)\u003d 0 ja x.<0f (x)<0, а при x.>0f (x)>0.
jaoks x.→ 0. Sel hetkel ei ole funktsiooni maksimaalselt minimaalselt. Tõesti, f (x)\u003d 0 ja x.<0f (x)<0, а при x.>0f (x)>0.

Seega võib ülaltoodud näidetest ja formuleeritud teoreemil näha, et funktsioon võib olla äärmuslik ainult kahel juhul: 1) punktides, kus tuletisinstrument on olemas ja null; 2) punktis, kus derivaat ei ole olemas.
Kui aga mingil hetkel x. 0 Me teame seda f "(x 0 ) \u003d 0, siis on võimatu järeldada, et punktis x. 0 funktsiooni on äärmuslik.
näiteks. ![]() .
.
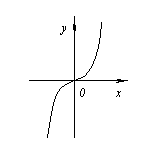
Kuid punkt x.\u003d 0 ei ole äärmuslik punkt, kuna selle punkti vasakpoolne funktsioon asub funktsiooni väärtus telje all Härg.ja ülaltoodud paremale.
Väärtused argumendi funktsiooni funktsiooni määramise funktsiooni, kus tuletatud funktsiooni kaebused null või ei eksisteeri, nimetatakse kriitilised punktid.
Eespool öeldut järeldub, et äärmuslike funktsioonide punktid on kriitiliste punktide hulgas ja mitte iga kriitiline punkt on äärmuslik punkt. Seetõttu peate äärmusliku funktsiooni leidmiseks leidma kõik funktsiooni kriitilised punktid ja seejärel igaüks neist punktidest uurivad eraldi maksimaalselt ja minimaalselt. Sest see on järgmine teoreem.
Teoreem 2. (piisav seisund eksperimendi olemasolu jaoks.) Olgu funktsioon pidevalt mõningase intervalliga, mis sisaldab kriitilist punkti x. 0 ja selle intervalli punktides diferentseeruvad (välja arvatud punkt ise x. 0). Kui liigute vasakult paremale, muudab derivaat märgi plussist miinus, seejärel punktis x. = x. 0 funktsioonil on maksimaalne. Kui ülemineku ajal läbi x. 0 vasakult paremale, derivaat muudab märk miinus pluss, funktsioonil on vähemalt minimaalne.
Seega, kui
Tõendid. Oletame kõigepealt, et liikudes x. 0 Tuletisinstrument muudab märk plussist miinus, st üleüldse x.Punkti lähedal x. 0 f "(x)\u003e0 x.< x 0 , f "(x)< 0 x\u003e X. 0. Rakenda Lagrange'i teoreemi vahe f (x) - f (x 0 ) \u003d F "c) (x- x 0) Kus c. Vajadus x. ja x. 0 .
Seega kõikide väärtuste puhul x. üsna lähedal k. x. 0 f (x)< f (x. 0 ) . Mis tähendab, et punktis x. 0 funktsioonil on maksimaalne.
Samamoodi on tõendatud minimaalse teoreemi teine \u200b\u200bosa.
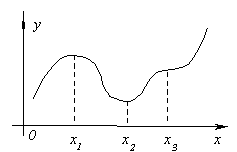
Me illustreerime selle teoreemi tähendust pildil. Las olla f "(x 1 ) \u003d 0 ja mis tahes xüsna lähedal k. x. 1, ebavõrdsus toimub
f "(x)< 0 nagu x.< x 1 , f "(x)\u003e0 nagu x\u003e X. 1 .
Siis vasakul poolel x. 1 funktsioon suureneb ja paremal väheneb, seetõttu x. = x. 1 funktsioon läbib kasvavast kahanevalt, st sellel on maksimaalne.
Samamoodi saate kaaluda punkte x. 2 I. x. 3 .

Skemaatiliselt võib kõik ülaltoodud pildil kujutada:
Uurimisfunktsiooni reegel Y \u003d F (x) esurm
Näited. Uurige funktsioone vähemalt ja maksimaalselt.
Funktsiooni suurimad ja väiksemad väärtused segmendis
Suur Tähenduses funktsiooni segmendis nimetatakse suurimaks selle segmendi kõikidest väärtustest ja väikseim - Kõigi selle väärtuste väikseim.
Mõtle funktsiooni y \u003d F (x) Pidev segmendis [ a, B.]. Nagu te teate, jõuab see funktsioon oma suurimate ja väikseimate väärtusteni või segmendi piirile või selle sees. Kui funktsiooni suurim või väikseim väärtus saavutatakse segmendi sisemises punktis, on see väärtus maksimaalne või minimaalne funktsioon, st saavutatakse kriitilistes punktides.
Seega saame järgmised reegel leida suurimate ja väikseimate väärtuste funktsiooni segmendis [ a, B.] :
Pöörake funktsiooni Y \u003d x 3 - 3x 2. Kaaluge punkti x \u003d 0 naabrust, st Mõni intervall, mis sisaldab seda punkti. On loogiline, et see on selline punkti x \u003d 0 naabruses, mis funktsiooni Y \u003d x 3 - 3X 2 kõige väärtuslikum väärtus võtab selles naabruses punktis x \u003d 0. Näiteks intervalliga (-1; 1) suurim väärtus 0, funktsioon võtab punkt x \u003d 0. Punkti x \u003d 0 nimetatakse selle funktsiooni maksimaalseks punktiks.
Samamoodi punkti x \u003d 2 nimetatakse punktile x 3 - 3x 2, kuna sellel hetkel ei ole funktsiooniväärtus suurem kui selle väärtus teise punkti x \u003d 2 naabruses, näiteks; Ümbrus (1,5; 2.5).
Seega nimetatakse maksimaalset punkti f (x) punkti x 0, kui on olemas punkt x 0 naabruses - nii, et ebavõrdsus f (x) ≤ f (x 0) teostatakse selle naabruskonna kõigi x jaoks.
Näiteks punkt x 0 \u003d 0 on maksimaalse funktsiooni F (x) \u003d 1 - x 2 punkt, kuna F (0) \u003d 1 ja ebavõrdsus F (x) ≤ 1 on tõsi kõikides väärtuses.
Minimaalse funktsiooni F (x) punktiini nimetatakse punkti x 0-le, kui on selline punkti x 0 naabruses, mis viiakse läbi ebavõrdsuse f (x) ≥ f (x 0) selle naabruskonna jaoks kõigi x jaoks.
Näiteks punkt x 0 \u003d 2 on minimaalne funktsioon f (x) \u003d 3 + (x-2) 2, kuna F (2) \u003d 3 ja f (x) ≥ 3 kõigi x jaoks.
Äärmuspunktid on minimaalse ja maksimaalse punkti punktid.
Me pöördume funktsiooni F (x), mis määratakse kindlaks mõnes punkti x 0 naabruses ja sellel hetkel derivaat.
Kui x 0 on diferentseeritava funktsiooni f (x), siis f "(x 0) \u003d 0. Seda avaldust nimetatakse talu teoreemile.
Põllumajandusettevõtte teoreemil on visuaalne geomeetriline tähendus: äärmuslikus punktis puutuja paralleelselt abscissa teljega ja seetõttu selle nurgategur
F "(x 0) on null.
Näiteks funktsioon F (x) \u003d 1 - 3x2 on punktis x 0 \u003d 0 maksimaalne, selle derivaat F "(x) \u003d -2x, f" (0) \u003d 0.
F (x) \u003d (x-2) 2 + 3 on minimaalne punkt x 0 \u003d 2, f "(x) \u003d 2 (x-2), f" (2) \u003d 0.
Pange tähele, et kui F "(x 0) \u003d 0, ei ole see piisav, et kinnitada, et x 0 on tingimata äärmiselt emmerma funktsiooni f (x).
Näiteks, kui F (x) \u003d x 3, siis f "(0) \u003d 0. Emmeväljaspunkti X \u003d 0 punkt ei ole, kuna funktsioon x 3 suureneb kogu numbrilisel teljel.
Niisiis tuleb äärmusliku diferentseeruva funktsiooni punkte otsida ainult võrrandi juurte seas
f "(x) \u003d 0, kuid selle võrrandi juur ei ole alati äärmuspunkt.
Statsionaarseid punkte nimetatakse punkte, kus tuletisinstrument on null.
Seega, et punkt x 0 olla äärmuslik, on vaja, et see on statsionaarne punkt.
Mõtle piisavalt tingimusi, et statsionaarne punkt on äärmuslik punkt, st Tingimused statsionaarse punkti teostamisel on minimaalse või maksimaalse funktsiooni punkt.
Kui vasakpoolse punkti derivaat on positiivne ja õigus on negatiivne, s.o. Tuletisinstrument muudab selle punkti kaudu sisselülitamisel "+" märk "+" allmärgile, see statsionaarne punkt on maksimaalne punkt.
Tõepoolest, sel juhul on statsionaarse punkti vasakpoolne funktsioon suureneb ja paremal - vähenemine, s.o. See punkt on maksimaalne punkt.
Kui tuletisinstrument muudab märk "-" allkirja "+" allmärgil liikudes läbi statsionaarse punkti, siis see statsionaarne punkt on minimaalne punkt.
Kui derivaat ei muutu statsionaarse punkti kaudu, st Vasakul ja paremal statsionaarse punkti, derivaat on positiivne või negatiivne, siis see punkt ei ole äärmuslik.
Kaaluge ühte ülesannetest. Leidke äärmusliku funktsiooni f (x) \u003d x 4 - 4x3.
Otsus.
1) Leia derivaat: F "(x) \u003d 4x 3 - 12x 2 \u003d 4x2 (x-3).
2) Leiame statsionaarseid punkte: 4x 2 (x - 3) \u003d 0, x 1 \u003d 0, x 2 \u003d 3.
3) Intervalli meetodit tõendab, et derivaat f "(x) \u003d 4x 2 (x-3) on positiivne x\u003e 3, negatiivne x< 0 и при 0 < х < 3.
4) Kuna vahetamisel punkti x 1 \u003d 0, derivaatmärk ei muutu, siis see punkt ei ole äärmuslik punkt.
5) Tuletisinstrument muudab märgi "-" märk "+" märk, kui lülitate punkti x 2 \u003d 3. Seetõttu x 2 \u003d 3 on minimaalne punkt.
kohapeal, täis- või osalise kopeerimise materjali viide algse allikas on vajalik.