In July 2020, NASA launches an expedition to Mars. The spacecraft will deliver an electronic media to Mars with the names of all registered expedition participants.

Registration of participants is open. Get your ticket for Mars for this link.

If this post decided your problem or just liked you, share a link to it with my friends on social networks.

One of these code options must be copied and insert into the code of your webpage, preferably between the tags and or immediately after the tag . According to the first version, MathJax is loaded faster and slows down the page. But the second option automatically tracks and loads the latest MathJax versions. If you insert the first code, it will need to be periodically updated. If you insert the second code, the pages will be loaded slower, but you will not need to constantly monitor MathJax updates.

Connect MathJax is the easiest way to Blogger or WordPress: Add a widget for inserting a third-party JavaScript code to insert the first or second version of the download code presented above and place the widget closer to the beginning of the template (by the way, it is not at all necessary Since the MathJax script is loaded asynchronously). That's all. Now read Mathml, Latex and Asciimathml markup syntax, and you are ready to insert mathematical formulas on the web pages of your site.

Another New Year's Eve ... Frosty Weather and Snowflakes on the window glass ... All this prompted me to again write about ... Fractals, and about what he knows about this Alpha tungshes. On this occasion, there is an interesting article in which there are examples of two-dimensional fractal structures. Here we will consider more complex examples of three-dimensional fractals.

The fractal can be clearly imagined (describe), as a geometric shape or body (having in mind that both there are many, in this case, a set of points), the details of which have the same shape as the original figure itself. That is, it is a self-like structure, considering the details of which with an increase, we will see the same form as without increasing. Whereas in the case of a conventional geometric shape (not fractal), with an increase we will see parts that have a simpler form than the original figure itself. For example, with a sufficiently large increase, the part of the ellipse looks like a straight line. With fractals, this does not happen: with any increases, we will again see the same complex shape, which will repeat again and again.

Benoit Mandelbrot (Benoit Mandelbrot), the founder of the science of fractals, in his article Fractals and art in the name of science wrote: "Fractals are geometric forms that are equally complex in their details, as in its general form. That is, if Part of the fractal will be increased to the size of the whole, it will look like an integer, or exactly, or, possibly, with a small deformation. "

Turn to the graph of the function y \u003d x 3 - 3x 2. Consider the neighborhood of the point x \u003d 0, i.e. Some interval containing this point. It is logical that there is such a neighborhood of the point x \u003d 0, which the most value of the function y \u003d x 3 - 3x 2 in this neighborhood takes at point x \u003d 0. For example, on the interval (-1; 1) the greatest value 0, the function takes At point x \u003d 0. The point x \u003d 0 is called the point of the maximum of this function.

Similarly, the point x \u003d 2 is called a point of a minimum function x 3 - 3x 2, since at this point the function value is not greater than its value at another point of the neighborhood of the point x \u003d 2, for example, the surroundings (1.5; 2.5).

Thus, the maximum point F (x) is called point x 0, if there is a neighborhood of the point X 0 - such that the inequality F (x) ≤ f (x 0) is performed for all x from this neighborhood.

For example, the point x 0 \u003d 0 is the point of the maximum function f (x) \u003d 1 - x 2, since f (0) \u003d 1 and the inequality F (x) ≤ 1 is true at all values.

The point of the minimum function f (x) is called point X 0, if there is such a neighborhood of the point x 0, which is carried out inequality f (x) ≥ f (x 0) for all x from this neighborhood.

For example, the point x 0 \u003d 2 is the point of the minimum function f (x) \u003d 3 + (x - 2) 2, since f (2) \u003d 3 and f (x) ≥ 3 for all x.

Points of extremum are the points of a minimum and a maximum point.

We turn to the function f (x), which is determined in some neighborhood of the point x 0 and has a derivative at this point.

If x 0 is the extremum point of the differentiable function f (x), then f "(x 0) \u003d 0. This statement is called the farm theorem.

The farm theorem has a visual geometric meaning: at the extremum point is tangent parallel to the abscissa axis and therefore its angular coefficient
F "(x 0) is zero.

For example, the function f (x) \u003d 1 - 3x 2 has at the point x 0 \u003d 0 maximum, its derivative F "(x) \u003d -2x, f" (0) \u003d 0.

The function f (x) \u003d (x - 2) 2 + 3 has a minimum at point x 0 \u003d 2, f "(x) \u003d 2 (x - 2), f" (2) \u003d 0.

Note that if f "(x 0) \u003d 0, this is not enough to assert that x 0 is a necessarily point of extremum function F (x).

For example, if f (x) \u003d x 3, then f "(0) \u003d 0. However, the point of the extremum point x \u003d 0 is not, since the function X 3 increases on the entire numeric axis.

So, the points of extremum differentiable function must be searched only among the roots of the equation
f "(x) \u003d 0, but the root of this equation is not always a point of extremum.

Stationary points are called points in which the derivative function is zero.

Thus, in order for the point x 0 to be an extremum point, it is necessary that it is a stationary point.

Consider sufficient conditions that the stationary point is an extremum point, i.e. Conditions when performing a stationary point is a point of a minimum or maximum function.

If the derivative of the leftmost point is positive, and the right is negative, i.e. The derivative changes the "+" sign on the "-" sign when switching through this point, this stationary point is a maximum point.

Indeed, in this case, the left of the stationary point is the function increases, and to the right - decrease, i.e. This point is a maximum point.

If the derivative changes the sign "-" on the "+" sign when moving through a stationary point, then this stationary point is a minimum point.

If the derivative does not change when switching through a stationary point, i.e. On the left and right of the stationary point, the derivative is positive or negative, then this point is not an extremum point.

Consider one of the tasks. Find the points of the extremum function f (x) \u003d x 4 - 4x 3.

Decision.

1) Find a derivative: F "(x) \u003d 4x 3 - 12x 2 \u003d 4x 2 (x - 3).

2) We will find stationary points: 4x 2 (x - 3) \u003d 0, x 1 \u003d 0, x 2 \u003d 3.

3) the interval method establishes that the derivative F "(x) \u003d 4x 2 (x - 3) is positive at x\u003e 3, negative at x< 0 и при 0 < х < 3.

4) Since when switching through the point x 1 \u003d 0, the derivative mark does not change, then this point is not an extremum point.

5) The derivative changes the sign "-" on the "+" sign when switching through the point x 2 \u003d 3. Therefore, x 2 \u003d 3 is a minimum point.

the site, with full or partial copying of the material reference to the original source is required.

Let the function $ z \u003d f (x, y) $ is defined in some neighborhood of the point $ (x_0, y_0) $. It is said that $ (x_0, y_0) $ - point (local) maximum, if for all points $ (x, y) $ of some neighborhood of the point $ (x_0, y_0) $ is performed inequality $ f (x, y)< f(x_0,y_0)$. Если же для всех точек этой окрестности выполнено условие $f(x,y)> F (x_0, y_0) $, then the point $ (x_0, y_0) $ is called a point (local) minimum.

Maximum and minimum points are often called a common term - extremum points.

If $ (x_0, y_0) $ is a maximum point, then the value of the function $ F (x_0, y_0) $ at this point is called the maximum function $ z \u003d f (x, y) $. Accordingly, the value of the function at a minimum point is called a minimum of the function $ z \u003d f (x, y) $. Minima and maxima function are combined by a common term - extremes of the function.

Algorithm research function $ z \u003d f (x, y) $ for extremum

1. Find the private derivatives of $ \\ FRAC (\\ Partial z) (\\ Partial x) $ and $ \\ FRAC (\\ Partial Z) (\\ Partial y) $. Create and solve the system of equations $ \\ left \\ (\\ begin (aligned) \\ FRAC (\\ Partial z) (\\ partial x) \u003d 0; \\\\ \\ FRAC (\\ Partial z) (\\ partial y) \u003d 0. \\ Find $ \\ FRAC (\\ Partial ^ 2z) (\\ Partial x ^ 2) $, $ \\ FRAC (\\ Partial ^ 2z) (\\ Partial x \\ Partial y) $, $ \\ FRAC (\\ Partial ^ 2Z) (\\ Partial y ^ 2) $ and calculate the value of $ \\ delta \u003d \\ FRAC (\\ Partial ^ 2z) (\\ partial x ^ 2) \\ CDOT \\ FRAC (\\ Partial ^ 2z) (\\ Partial Y ^ 2) - \\ Left (\\ FRAC (\\ Partial ^ 2z) (\\ Partial X \\ Partial Y) \\ Right) ^ 2 $ in each stationary point. After that, use the following scheme:
2. If $ \\ Delta\u003e 0 $ and $ \\ FRAC (\\ Partial ^ 2z) (\\ Partial x ^ 2)\u003e 0 $ (or $ \\ FRAC (\\ Partial ^ 2z) (\\ Partial Y ^ 2)\u003e 0 $), That in the test point is a minimum point.
   1. If $ \\ Delta\u003e 0 $ and $ \\ FRAC (\\ Partial ^ 2z) (\\ Partial x ^ 2)
   2. If $ \\ Delta< 0$ (или $\frac{\partial^2z}{\partial y^2} < 0$), то в исследуемая точка есть точкой максимума.
   3. If $ \\ delta \u003d 0 $, then nothing definite about the presence of extremum cannot be said; Additional research is required.< 0$, то в расматриваемой стационарной точке экстремума нет.
   4. Note (desirable for a more complete text understanding): show / hide

{!LANG-3367eb1d375bb4c14b007571166d0479!}

If $ \\ delta\u003e 0 $, then $ \\ FRAC (\\ Partial ^ 2z) (\\ Partial x ^ 2) \\ Cdot \\ FRAC (\\ Partial ^ 2z) (\\ Partial Y ^ 2) - \\ left (\\ FRAC (\\ And hence it follows that $ \\ FRAC (\\ Partial ^ 2z) (\\ Partial x ^ 2) \\ CDOT \\ FRAC (\\ Partial ^ 2z) (\\ Partial y ^ 2)\u003e \\ left (\\ FRAC (\\ Partial ^ 2z) (\\ Partial x \\ Partial y) \\ Right) ^ 2 ≥ 0 $. Those. $ \\ FRAC (\\ Partial ^ 2z) (\\ Partial x ^ 2) \\ CDOT \\ FRAC (\\ Partial ^ 2z) (\\ Partial y ^ 2)\u003e 0 $. If the product of certain values \u200b\u200bare more than zero, then these values \u200b\u200bof one sign. Those., For example, if $ \\ FRAC (\\ Partial ^ 2z) (\\ Partial x ^ 2)\u003e 0 $, then $ \\ FRAC (\\ Partial ^ 2z) (\\ Partial y ^ 2)\u003e 0 $. In short, if $ \\ Delta\u003e 0 $ is the signs of $ \\ FRAC (\\ Partial ^ 2z) (\\ Partial x ^ 2) $ and $ \\ FRAC (\\ Partial ^ 2z) (\\ Partial y ^ 2) $ coincide.

Example №1

Explore the Extreme function $ z \u003d 4x ^ 2-6xy-34x + 5y ^ 2 + 42y + $ 7.

$$ \\ FRAC (\\ Partial z) (\\ Partial x) \u003d 8x-6y-34; \\ FRAC (\\ Partial z) (\\ Partial y) \u003d - 6x + 10y + 42. $$.

$$ \\ left \\ (\\ begin (aligned) & 8x-6y-34 \u003d 0; \\\\ & -6x + 10y + 42 \u003d 0. \\ End (Aligned) \\ Right. $$

We will reduce each equation of this system by $ 2 $ and transferring the numbers to the right parts of the equations:

$$ \\ left \\ (\\ begin (aligned) & 4x-3y \u003d 17; \\\\ & -3x + 5y \u003d -21. \\ END (Aligned) \\ Right. $$

We received a system of linear algebraic equations. In this situation, it seems to me the most convenient use of the Cramer method to solve the system obtained.

$$ \\ Begin (Aligned) & \\ Delta \u003d \\ Left | \\ Begin (Array) (CC) 4 & -3 \\\\ -3 & 5 \\ END (Array) \\ Right | \u003d 4 \\ CDOT 5 - (- 3) \\ Cdot (-3) \u003d 20-9 \u003d 11; \\ \\ Begin (Array) (CC) 17 & -3 \\\\ -21 & 5 \\ END (Array) \\ Right | \u003d 17 \\ CDot 5 - (- 3) \\ Cdot (-21) \u003d 85-63 \u003d 22; \\ \\ Begin (Array) (CC) 4 & 17 \\\\ -3 & -21 \\ END (Array) \\ Right | \u003d 4 \\ Cdot (-21) -17 \\ Cdot (-3) \u003d - 84 + 51 \u003d -33 . \\ END (aligned) \\\\ x \u003d \\ FRAC (\\ Delta_ (x)) (\\ Delta) \u003d \\ FRAC (22) (11) \u003d 2; \\; Y \u003d \\ FRAC (\\ Delta_ (Y)) (\\ Delta) \u003d \\ FRAC (-33) (11) \u003d - 3. $$.

The values \u200b\u200bof $ x \u003d $ 2, $ y \u003d -3 $ are the coordinates of the stationary point $ (2; -3) $.

$$ \\ FRAC (\\ Partial ^ 2 z) (\\ Partial x ^ 2) \u003d 8; \\ FRAC (\\ Partial ^ 2 z) (\\ Partial y ^ 2) \u003d 10; \\ FRAC (\\ Partial ^ 2 z) (\\ Partial x \\ Partial y) \u003d - 6. $$.

Calculate the value of $ \\ delta $:

$$ \\ Delta \u003d \\ FRAC (\\ Partial ^ 2z) (\\ Partial x ^ 2) \\ CDOT \\ FRAC (\\ Partial ^ 2z) (\\ Partial Y ^ 2) - \\ Left (\\ FRAC (\\ Partial ^ 2Z) ( \\ Partial X \\ Partial y) \\ RIGHT) ^ 2 \u003d 8 \\ CDOT 10 - (- 6) ^ 2 \u003d 80-36 \u003d 44. $$.

Since $ \\ Delta\u003e 0 $ and $ \\ FRAC (\\ Partial ^ 2 z) (\\ Partial x ^ 2)\u003e 0 $, then according to the $ (2; -3) $ there is a point of a minimum function $ z $. The minimum function is $ z $ will find, substituting the coordinate of the point $ (2; -3) $:

$$ z_ (min) \u003d z (2; -3) \u003d 4 \\ CDOT 2 ^ 2-6 \\ CDOT 2 \\ CDOT (-3) -34 \\ CDOT 2 + 5 \\ CDOT (-3) ^ 2 + 42 \\ $$.

Answer: $ (2; -3) $ - minimum point; $ z_ (min) \u003d - 90 $.

Example number 2.

Examine on the extremum function $ z \u003d x ^ 3 + 3XY ^ 2-15x-12y + $ 1.

We will follow the above. To begin to find private derivatives of the first order:

$$ \\ FRAC (\\ Partial z) (\\ Partial x) \u003d 3x ^ 2 + 3Y ^ 2-15; \\ FRAC (\\ Partial z) (\\ Partial y) \u003d 6XY-12. $$.

We will make a system of equations $ \\ left \\ (\\ begin (aligned) \\ FRAC (\\ Partial z) (\\ Partial x) \u003d 0; \\\\ & \\ FRAC (\\ Partial z) (\\ Partial y) \u003d 0. \\ END ( Aligned) \\ Right. $:

$$ \\ left \\ (\\ begin (aligned) & 3x ^ 2 + 3Y ^ 2-15 \u003d 0; \\\\ & 6XY-12 \u003d 0. \\ END (ALIGNED) \\ RIGHT. $$

Sperate the first equation by 3, and the second - by 6.

$$ \\ left \\ (\\ begin (aligned) & x ^ 2 + y ^ 2-5 \u003d 0; \\\\ & xy-2 \u003d 0. \\ END (ALIGNED) \\ RIGHT. $$

If $ x \u003d 0 $, then the second equation will lead us to a contradiction: $ 0 \\ Cdot y-2 \u003d 0 $, $ -2 \u003d 0 $. Hence the output: $ X \\ NEQ 0 $. Then, from the second equation, we have: $ xy \u003d 2 $, $ y \u003d \\ FRAC (2) (x) $. Substituting $ Y \u003d \\ FRAC (2) (x) $ in the first equation, we will have:

$$ x ^ 2 + \\ left (\\ FRAC (2) (X) \\ RIGHT) ^ 2-5 \u003d 0; \\\\ x ^ 2 + \\ FRAC (4) (x ^ 2) -5 \u003d 0; \\\\ $$.

Received a biquette equation. We make a replacement $ t \u003d x ^ 2 $ (while we mean that $ T\u003e 0 $):

$$ T ^ 2-5T + 4 \u003d 0; \\\\ \\ begin (aligned) & d \u003d (- 5) ^ 2-4 \\ Cdot 1 \\ Cdot 4 \u003d 9; \\\\ & T_1 \u003d \\ FRAC (- (- 5) - \\ SQRT (9)) (2) \u003d \\ FRAC (5-3) (2) \u003d 1; \\\\ & T_2 \u003d \\ FRAC (- (- 5) + \\ sqrt (9)) (2) \u003d \\ FRAC (5 + 3) (2) \u003d 4. \\ End (Aligned) $$

If $ t \u003d 1 $, then $ x ^ 2 \u003d 1 $. From here we have two values \u200b\u200bof $ x $: $ x_1 \u003d 1 $, $ x_2 \u003d -1 $. If $ T \u003d $ 4, then $ x ^ 2 \u003d $ 4, i.e. $ x_3 \u003d $ 2, $ x_4 \u003d -2 $. Remembering that $ Y \u003d \\ FRAC (2) (X) $, we get:

\\ begin (aligned) & y_1 \u003d \\ FRAC (2) (x_1) \u003d \\ FRAC (2) (1) \u003d 2; \\\\ & y_2 \u003d \\ FRAC (2) (x_2) \u003d \\ FRAC (2) (- 1 ) \u003d - 2; \\\\ & y_3 \u003d \\ FRAC (2) (x_3) \u003d \\ FRAC (2) (2) \u003d 1; \\\\ & y_4 \u003d \\ FRAC (2) (x_4) \u003d \\ FRAC (2) ( -2) \u003d - 1. \\ End (Aligned)

So, we have four stationary points: $ M_1 (1; 2) $, $ M_2 (-1; -2) $, $ M_3 (2; 1) $, $ M_4 (-2; -1) $. This is the first step of the algorithm over.

Now proceed to the algorithm. Find the second-order private derivatives:

$$ \\ FRAC (\\ Partial ^ 2 z) (\\ Partial x ^ 2) \u003d 6x; \\ FRAC (\\ Partial ^ 2 z) (\\ partial y ^ 2) \u003d 6x; \\ FRAC (\\ Partial ^ 2 z) (\\ Partial x \\ Partial y) \u003d 6Y. $$.

Find $ \\ Delta $:

$$ \\ Delta \u003d \\ FRAC (\\ Partial ^ 2z) (\\ Partial x ^ 2) \\ CDOT \\ FRAC (\\ Partial ^ 2z) (\\ Partial Y ^ 2) - \\ Left (\\ FRAC (\\ Partial ^ 2Z) ( \\ Partial x \\ Partial y) \\ Right) ^ 2 \u003d 6x \\ Cdot 6x- (6Y) ^ 2 \u003d 36x ^ 2-36Y ^ 2 \u003d 36 (x ^ 2-y ^ 2). $$.

Now we will calculate the value of $ \\ delta $ in each of the previously found stationary points. Let's start from the point $ M_1 (1; 2) $. At this point we have: $ \\ delta (m_1) \u003d 36 (1 ^ 2-2 ^ 2) \u003d - $ 108. Since $ \\ Delta (M_1)< 0$, то согласно в точке $M_1$ экстремума нет.

We explore the point $ M_2 (-1; -2) $. At this point we have: $ \\ delta (m_2) \u003d 36 ((- 1) ^ 2 - (- 2) ^ 2) \u003d - $ 108. Since $ \\ Delta (M_2)< 0$, то согласно в точке $M_2$ экстремума нет.

We explore the point $ M_3 (2; 1) $. At this point we get:

$$ \\ DELTA (M_3) \u003d 36 (2 ^ 2-1 ^ 2) \u003d 108; \\; \\; \\ left. \\ FRAC (\\ Partial ^ 2 z) (\\ Partial x ^ 2) \\ Right | _ (M_3) \u003d 6 \\ Cdot 2 \u003d 12. $$.

Since $ \\ Delta (M_3)\u003e 0 $ and $ \\ left. \\ FRAC (\\ Partial ^ 2 z) (\\ Partial x ^ 2) \\ Right | _ (M_3)\u003e 0 $, then according to $ M_3 (2; 1) $ There is a point of a minimum function $ z $. At least the function of $ z $ will find, substituting the coordinate point of $ M_3 in the specified function:

$$ z_ (min) \u003d z (2; 1) \u003d 2 ^ 3 + 3 \\ CDOT 2 \\ CDOT 1 ^ 2-15 \\ CDOT 2-12 \\ CDOT 1 + 1 \u003d -27. $$.

It remains to explore the $ M_4 (-2; -1) $ point. At this point we get:

$$ \\ DELTA (M_4) \u003d 36 ((- 2) ^ 2 - (- 1) ^ 2) \u003d 108; \\; \\; \\ left. \\ FRAC (\\ Partial ^ 2 z) (\\ Partial x ^ 2) \\ Right | _ (m_4) \u003d 6 \\ Cdot (-2) \u003d - 12. $$.

Since $ \\ Delta (M_4)\u003e 0 $ and $ \\ left. \\ FRAC (\\ Partial ^ 2 z) (\\ Partial x ^ 2) \\ Right | _ (M_4)< 0$, то согласно $M_4(-2;-1)$ есть точкой максимума функции $z$. Максимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_4$:

$$ z_ (max) \u003d z (-2; -1) \u003d (- 2) ^ 3 + 3 \\ Cdot (-2) \\ Cdot (-1) ^ 2-15 \\ CDOT (-2) -12 \\ CDOT (-1) + 1 \u003d 29. $$.

Research on the extremum is completed. It remains only to record the answer.

Answer:

• $ (2; 1) $ - a minimum point, $ z_ (min) \u003d - 27 $;
• $ (- 2; -1) $ - Maximum point, $ z_ (max) \u003d $ 29.

Note

Calculate the value of $ \\ Delta $ in the general case is not necessary, because we are only interested in the sign, and not the specific value of this parameter. For example, for the example discussed above, No. 2 at point $ M_3 (2; 1) $ we have $ \\ delta \u003d 36 \\ Cdot (2 ^ 2-1 ^ 2) $. It is obvious here that $ \\ delta\u003e 0 $ (as both factors $ 36 $ and $ (2 ^ 2-1 ^ 2) $ are positive) and you can not find a specific value of $ \\ Delta $. True, for typical calculations, this remark is useless - they require to bring the calculation to the number :)

Example number 3.

Investigate on the extremum function $ z \u003d x ^ 4 + y ^ 4-2x ^ 2 + 4xy-2y ^ 2 + 3 $.

We will follow. To begin to find private derivatives of the first order:

$$ \\ FRAC (\\ Partial Z) (\\ Partial x) \u003d 4x ^ 3-4x + 4y; \\ FRAC (\\ Partial z) (\\ Partial y) \u003d 4Y ^ 3 + 4x-4y. $$.

We will make a system of equations $ \\ left \\ (\\ begin (aligned) \\ FRAC (\\ Partial z) (\\ Partial x) \u003d 0; \\\\ & \\ FRAC (\\ Partial z) (\\ Partial y) \u003d 0. \\ END ( Aligned) \\ Right. $:

$$ \\ left \\ (\\ begin (aligned) & 4x ^ 3-4x + 4y \u003d 0; \\\\ & 4Y ^ 3 + 4x-4y \u003d 0. \\ End (Aligned) \\ Right. $$

We will reduce both equations for $ 4 $:

$$ \\ left \\ (\\ begin (aligned) & x ^ 3-x + y \u003d 0; \\\\ & y ^ 3 + x-y \u003d 0. \\ End (Aligned) \\ Right. $$

Add to the second equation first and express $ y $ than $ x $:

$$ y ^ 3 + x-y + (x ^ 3-x + y) \u003d 0; \\\\ y ^ 3 + x ^ 3 \u003d 0; y ^ 3 \u003d -x ^ 3; y \u003d -x. $$.

Substituting $ Y \u003d -x $ in the first equation of the system, we will have:

$$ x ^ 3-x-x \u003d 0; \\\\ x ^ 3-2x \u003d 0; \\\\ x (x ^ 2-2) \u003d 0. $$.

From the resulting equation, we have: $ x \u003d 0 $ or $ x ^ 2-2 \u003d 0 $. From the equation $ x ^ 2-2 \u003d 0 $ it follows that $ x \u003d - \\ sqrt (2) $ or $ x \u003d \\ sqrt (2) $. So, there are three values \u200b\u200bof $ x $, namely: $ x_1 \u003d 0 $, $ x_2 \u003d - \\ sqrt (2) $, $ x_3 \u003d \\ sqrt (2) $. Since $ y \u003d -x $, then $ y_1 \u003d -x_1 \u003d 0 $, $ y_2 \u003d -x_2 \u003d \\ sqrt (2) $, $ y_3 \u003d -x_3 \u003d - \\ sqrt (2) $.

The first step of the solution is over. We got three stationary points: $ M_1 (0; 0) $, $ m_2 (- \\ sqrt (2), \\ sqrt (2)) $, $ M_3 (\\ SQRT (2), - \\ SQRT (2)) $ .

Now proceed to the algorithm. Find the second-order private derivatives:

$$ \\ FRAC (\\ Partial ^ 2 z) (\\ Partial x ^ 2) \u003d 12x ^ 2-4; \\ FRAC (\\ Partial ^ 2 z) (\\ Partial y ^ 2) \u003d 12y ^ 2-4; \\ FRAC (\\ Partial ^ 2 z) (\\ Partial x \\ Partial y) \u003d 4. $$.

Find $ \\ Delta $:

$$ \\ Delta \u003d \\ FRAC (\\ Partial ^ 2z) (\\ Partial x ^ 2) \\ CDOT \\ FRAC (\\ Partial ^ 2z) (\\ Partial Y ^ 2) - \\ Left (\\ FRAC (\\ Partial ^ 2Z) ( \\ Partial x \\ Partial y) \\ Right) ^ 2 \u003d (12x ^ 2-4) (12Y ^ 2-4) -4 ^ 2 \u003d \\\\ \u003d 4 (3x ^ 2-1) \\ CDOT 4 (3Y ^ 2 -1) -16 \u003d 16 (3x ^ 2-1) (3Y ^ 2-1) -16 \u003d 16 \\ CDOT ((3x ^ 2-1) (3Y ^ 2-1) -1). $$.

Now we will calculate the value of $ \\ delta $ in each of the previously found stationary points. Let's start from the point $ M_1 (0; 0) $. At this point we have: $ \\ delta (M_1) \u003d 16 \\ CDOT ((3 \\ Cdot 0 ^ 2-1) (3 \\ Cdot 0 ^ 2-1) -1) \u003d 16 \\ Cdot 0 \u003d 0 $. Since $ \\ Delta (M_1) \u003d 0 $, according to an additional study, it is impossible to say anything defined about the presence of extremum in the point in question. Let us drop this point alone and move in other points.

We investigate the point $ M_2 (- \\ SQRT (2), \\ SQRT (2)) $. At this point we get:

\\ Begin (Aligned) \\ Delta (M_2) \u003d 16 \\ CDOT ((3 \\ CDOT (- \\ SQRT (2)) ^ 2-1) (3 \\ CDOT (\\ SQRT (2)) ^ 2-1) - 1) \u003d 16 \\ CDOT 24 \u003d 384; \\\\ \\ LEFT. \\ FRAC (\\ Partial ^ 2 z) (\\ Partial x ^ 2) \\ Right | _ (M_2) \u003d 12 \\ CDOT (- \\ SQRT (2) ) ^ 2-4 \u003d 24-4 \u003d 20. \\ End (Aligned)

Since $ \\ Delta (M_2)\u003e 0 $ and $ \\ left. \\ FRAC (\\ Partial ^ 2 z) (\\ Partial x ^ 2) \\ Right | _ (M_2)\u003e 0 $, then according to $ M_2 (- \\ At least the function of $ z $ will find, substituting in the specified function of the coordinate point $ M_2 $:

$$ z_ (min) \u003d z (- \\ sqrt (2), \\ sqrt (2)) \u003d (- \\ sqrt (2)) ^ 4 + (\\ SQRT (2)) ^ 4-2 (- \\ sqrt ( 2)) ^ 2 + 4 \\ CDOT (- \\ SQRT (2)) \\ SQRT (2) -2 (\\ sqrt (2)) ^ 2 + 3 \u003d -5. $$.

Similar to the previous paragraph, we investigate the point $ M_3 (\\ SQRT (2), - \\ SQRT (2)) $. At this point we get:

\\ begin (Aligned) \\ Delta (M_3) \u003d 16 \\ CDOT ((3 \\ CDOT (\\ SQRT (2)) ^ 2-1) (3 \\ CDOT (- \\ SQRT (2)) ^ 2-1) - 1) \u003d 16 \\ CDOT 24 \u003d 384; \\\\ \\ LEFT. \\ FRAC (\\ Partial ^ 2 z) (\\ Partial x ^ 2) \\ Right | _ (M_3) \u003d 12 \\ CDOT (\\ SQRT (2)) ^ 2-4 \u003d 24-4 \u003d 20. \\ End (Aligned)

Since $ \\ Delta (M_3)\u003e 0 $ and $ \\ left. \\ FRAC (\\ Partial ^ 2 z) (\\ Partial x ^ 2) \\ Right | _ (M_3)\u003e 0 $, then according to $ M_3 (\\ SQRT (2) - \\ SQRT (2)) $ There is a point of a minimum function $ z $. At least the function of $ z $ will find, substituting the coordinate point of $ M_3 in the specified function:

$$ z_ (min) \u003d z (\\ sqrt (2), - \\ sqrt (2)) \u003d (\\ sqrt (2)) ^ 4 + (- \\ sqrt (2)) ^ 4-2 (\\ SQRT (2 )) ^ 2 + 4 \\ Cdot \\ SQRT (2) (- \\ SQRT (2)) - 2 (- \\ sqrt (2)) ^ 2 + 3 \u003d -5. $$.

It has arrived back to the point $ M_1 (0; 0) $, in which $ \\ Delta (M_1) \u003d 0 $. Additional research is required. Under this evasive phrase is meant "Do what you want" :). There is no general way to resolve such situations - and this is understandable. If such a way was, he would long come to all textbooks. And Pesima has to look for a special approach to each point in which $ \\ delta \u003d 0 $. Well, let's share the behavior of the function in the neighborhood of the point $ M_1 (0; 0) $. Immediately note that $ z (m_1) \u003d z (0; 0) \u003d $ 3. Suppose $ M_1 (0; 0) $ is a minimum point. Then for any point $ m $ from some neighborhood of the point $ M_1 (0; 0) $ we obtain $ z (m)\u003e z (m_1) $, i.e. $ z (m)\u003e $ 3. And what if any neighborhood contains the points in which $ z (M)< 3$? Тогда в точке $M_1$ уж точно не будет минимума.

Consider the points whose $ y \u003d 0 $, i.e. Points of type $ (x, 0) $. At these points, the $ z $ function will take such values:

$$ z (x, 0) \u003d x ^ 4 + 0 ^ 4-2x ^ 2 + 4x \\ Cdot 0-2 \\ Cdot 0 ^ 2 + 3 \u003d x ^ 4-2x ^ 2 + 3 \u003d x ^ 2 (x ^ 2-2) +3. $$.

In all sufficiently small surroundings $ M_1 (0; 0) $ we have $ x ^ 2-2< 0$, посему $x^2(x^2-2) < 0$, откуда следует $x^2(x^2-2)+3 < 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z < 3$, посему точка $M_1(0;0)$ не может быть точкой минимума.

But maybe the point $ M_1 (0; 0) $ is the maximum point? If so, then for any point $ m $ from some neighborhood of the point $ M_1 (0; 0) $ we get $ z (M)< z(M_1) $, т.е. $z(M) < 3$. А вдруг любая окрестность содержит точки, в которых $z(M) > $ 3? Then at point $ M_1 $ will definitely not be a maximum.

Consider the points whose $ y \u003d x $, i.e. The points of the form $ (x, x) $. At these points, the $ z $ function will take such values:

$$ z (x, x) \u003d x ^ 4 + x ^ 4-2x ^ 2 + 4x \\ cdot x-2 \\ cdot x ^ 2 + 3 \u003d 2x ^ 4 + 3. $$.

Since in any neighborhood of the point $ M_1 (0; 0) $ we have $ 2x ^ 4\u003e 0 $, then $ 2x ^ 4 + 3\u003e $ 3. Conclusion: Any neighborhood of a point $ M_1 (0; 0) $ contains the points in which $ z\u003e $ 3, therefore the point $ M_1 (0; 0) $ cannot be a maximum point.

Point $ M_1 (0; 0) $ is not a point of maximum, no point of minimum. Conclusion: $ M_1 $ is generally not an extremum point.

Answer: $ (- \\ sqrt (2), \\ sqrt (2)) $, $ (\\ SQRT (2), - \\ SQRT (2)) $ - minimum points $ z $. In both points $ z_ (min) \u003d - $ 5.

An important concept in mathematics is a function. With its help, you can clearly present many processes occurring in nature, reflect using formulas, tables and images on the graph of the relationship between certain values. An example is the dependence of the fluid layer pressure on the body from the depth of immersion, acceleration - from the action to the object of a certain force, increase the temperature - from the transmitted energy and many other processes. Research Features involves building a schedule, finding out its properties, areas of definition and values, increasing and descending gaps. An important point in this process is to find extremum points. About how to do it right, and a conversation next.

About the concept itself on a concrete example

In medicine, building a function of a function can tell about the progress of the disease in the patient's body, visually reflecting his condition. Suppose, on the axis oh, the time is postponed in days, and along the OU axis - the temperature of the human body. In the figure it is clearly seen how this indicator rises sharply, and then falls. It is not difficult to notice special points that reflect the moments when the function, previously, starts to decrease, and vice versa. These are points of extremum, that is, critical values \u200b\u200b(maximum and minimum) in this case of the patient's temperature, after which changes occur in its state.

Tilt angle

It can be easily determined in the figure as the derived function changes. If direct lines of graphics are going up, then it is positive. And than they are cooler, the greater the derivative takes, as the angle of inclination grows. During the periods of descending, this value takes negative values, at the extremum points turning to zero, and the graph of the derivative in the latter case is drawn parallel to the axis oh.

Any other process should be considered in the same way. But the best thing about this concept can tell the movement of various bodies, visually shown in the charts.

Traffic

Suppose some object is moving in a straight line, evenly gaining speed. During this period, the change in the coordinate of the body graphically represents a certain curve, which mathematician would call the parabola branch. At the same time, the function is constantly increasing, since the indicators of the coordinate with each second change more quickly. The speed schedule demonstrates the behavior of the derivative, the value of which also increases. So, the movement does not have critical points.

So it continued indefinitely for a long time. But if the body suddenly decides to slow down, stop and start moving in another direction? In this case, the indices of the coordinates will begin to decrease. And the function will turn critical and from the increasing will turn into a decreasing.

In this example, it can be understood again that extremum points on the function graph appear at the moments when it ceases to be monotonous.

Physical sense derivative

The previously described showed that the essence derivative is the speed of change of function. In this clarification and its physical meaning is concluded. Extremum points are critical areas on the schedule. It is possible to find out and detect, calculate the value of the derivative, which turns out to be zero.

There is another sign that is a sufficient condition for extremum. The derivative in such places of inflection changes its sign: with "+" to "-" in the region of the maximum and with "-" on "+" in the area of \u200b\u200ba minimum.

Movement influenced by the strength of attraction

Imagine another situation. Children playing the ball, threw it in such a way that he began to move at an angle to the horizon. At the initial moment, the speed of this object was the largest, but under the action of gravity began to decrease, and with each second one and the same value of approximately 9.8 m / s 2. This is the meaning of acceleration arising under the influence of earthly gravity at a free fall. On the moon it would be about six times less.

A graph describing the movement of the body is a parabola with branches directed down. How to find extremum points? In this case, this is the top of the function, where the body speed (ball) takes the zero value. The derivative function becomes equal to zero. At the same time, the direction, and therefore, and the speed value changes to the opposite. The body flies down with every second faster, and accelerates to the same value - 9.8 m / s 2.

Second derivative

In the previous case, the speed module graph is drawn as straight. This line turns out first pointing down, since the value of this magnitude is constantly decreasing. Having achieved zero into one of the time, then the indicators of this value begin to increase, and the direction of graphic image of the speed module changes radically. Now the line is directed up.

Speed, being derived from the coordinate in time, also has a critical point. In this area, the function, first decreasing, begins to increase. This is the place of the point of extremum derived function. In this case, the tilt angle becomes equal to zero. And the acceleration, being the second derivative of the coordinate in time, changes the sign from "-" to "+". And the movement from the equilibrium becomes equal.

Schedule acceleration

Now consider four drawings. Each of them is displayed a graph of change over time of such a physical size as acceleration. In the case of "A", it remains positive and constant. This means that the body's speed, as well as its coordinate, is constantly increasing. If you submit that the object will move thus infinitely for a long time, the function reflecting the dependence of the coordinate from time to time will be ever increasing. It follows from this that it does not have critical areas. Extremum points on a derivative chart, that is, linearly changing speed is also missing.

The same applies to the case of "b" with a positive and ever-increasing acceleration. True, graphics for the coordinates and speed here will be somewhat more complicated.

When acceleration tends to zero

Considering the drawing "B", one can observe a completely different picture, which characterizes the movement of the body. His speed graphically will be depicted with a parabola with branches directed down. If you continue the line describing the change in acceleration before crossing it with the axis OH, and further, you can imagine that before this critical value, where the acceleration turns out to be zero, the object speed will increase everything slower. The extremum point derived from the coordinate function will be just at the top of the parabola, after which the body dramatically change the nature of the movement and starts moving in another direction.

In the latter case, "G", the nature of the movement is definitely determined. It only knows that there is no acceleration for some periods in question. So, the object can remain in place or movement occurs at a constant speed.

Task for the addition of coordinates

Let us turn to the tasks that are often found when studying algebra at school and are offered to prepare for the exam. In the figure, which is presented below, is depicted a graph of a function. It is required to calculate the amount of extremum points.

We will do it for the axis of the ordinate, by defining the coordinates of the critical areas, where the change in the characteristics of the function is observed. Simply put, we will find the values \u200b\u200bon the axis Oh for the beggar points, and then turn to the addition of the members received. According to the graph, it is obvious that they take the following values: -8; -7; -five; -3; -2; one; 3. In sum, this is -21, which is the answer.

Optimal solution

It is not necessary to explain how important the choice of optimal solution can be important. After all, the ways to achieve goals are a lot, but the best way out is usually one. This is extremely necessary, for example, when designing vessels, spacecraft and aircraft, architectural structures for finding the optimal form of data of man-made objects.

The speed of movement means largely depends on the competent information to the minimum of resistance, which they are tested when moving along water and air, from overloads arising from the action of gravitational forces and many other indicators. The ship is needed by such qualities such as stability during a storm, a minimum sediment is important for the river vessel. When calculating the optimal design of the extremum point on the chart, an idea of \u200b\u200bthe best solution of a complex problem can be given. The tasks of such a plan are often solved in the economy, in economic areas, in a variety of other life situations.

From ancient history

The tasks of the extremum occupied even the ancient wise men. Greek scientists successfully solved the mystery of the squares and volumes by mathematical computing. This is the first to understand that on the plane from a variety of figures with the same perimeter, the greatest area always has a circle. Similarly, the ball is endowed with the maximum volume among other items in space with the same surface. Solving such tasks were devoted to such famous personalities as Archimedes, Euclidean, Aristotle, Apollonius. Finding the points of the extremum perfectly managed to Geron, who resorted to the calculations, built ingenious devices. These include automata transported by steam, working on the same principle of pumps and turbines.

Construction of Carthagene

There is a legend, the plot of which is built on solving one of the extreme tasks. The result of a business approach, which demonstrated the Phoenician Tsarevna, who applied for help to the sages, was the construction of Carthage. The land plot for this ancient and illustrious city presented Didon (so called the government) the leader of one of the African tribes. The area of \u200b\u200bthe station did not seem first to him very large, since according to the Agreement it was supposed to be covered with a whirlpool. But Tsarevna commanded his warriors to cut it on thin stripes and make a belt from them. It turned out so long that she covered the site where the whole city was fitted.

The origins of mathematical analysis

And now we are transferred from ancient times in a later era. Interestingly, to awareness of the foundations of mathematical analysis pushed Kepler in the XVII century meeting with the seller of wine. The merchant was so knowledgeable in his profession, which could easily determine the volume of the beverage located in the barrel, simply dropping the iron harness there. Reflecting on such a curiosity, the famous scientist managed to solve this dilemma for himself. It turns out that the skillful phosters of those times came out to make vessels in such a way that at a certain height and radius of the circumference of the fastening rings they had a maximum capacity.

It became for Kepler reason for further reflection. The Bochara came to the optimal solution by the method of long search, errors and new attempts, transmitting their experience from generation to generation. But Kepler wanted to speed up the process and learn how to do the same in a short time by mathematical computing. All his developments, praised by colleagues, turned into the currently known theorems of Farm and Newton - Labitsa.

The task of finding the maximum area

Imagine that we have a wire, the length of which is 50 cm. How to make a rectangle, which has the greatest area from it?

Starting a solution should be proceeding from simple and known to any truth. It is clear that the perimeter of our figure will be 50 cm. It also develops from the doubted lengths of both sides. This means that, designated for "x" one of them, one of them is possible to express both (25 - x).

From here we get the area equal to x (25 - x). This expression can be represented as a function that accepts many values. The solution to the task requires to find the maximum of them, which means you should find out the extremum points.

To do this, we find the first derivative and equate it to zero. As a result, a simple equation is obtained: 25 - 2x \u003d 0.

From it we learn that one of the parties x \u003d 12.5.

Consequently, the other: 25 - 12.5 \u003d 12.5.

It turns out that the solution will be a square with a side of 12.5 cm.

How to find maximum speed

Consider another example. Imagine that there is a body, the rectilinear movement of which is described by the equation S \u003d - T 3 + 9T 2 - 24T - 8, where the distance passed is expressed in meters, and time in seconds. It is required to find the maximum speed. How to do it? I downloaded the speed, that is, the first derivative.

We obtain the equation: V \u003d - 3T 2 + 18T - 24. Now to solve the problem, you need to find extremum points. It is necessary to do this in the same way as in the previous task. We find the first derivative of speed and equate it to zero.

We get: - 6t + 18 \u003d 0. Hence the T \u003d 3 s. This is the time when the body speed takes a critical value. We substitute the resulting velocity given to the equation and obtain: v \u003d 3 m / s.

But how to understand that this is exactly the maximum speed, because the critical points of the function may be the greatest or smallest values? To check, you need to find the second derivative of speed. It is expressed by a number of 6 with a minus sign. This means that the found point is the maximum. And in the case of positive value, the second derivative would be at least. So, the solution found was correct.

The tasks given as an example are only part of those that can be solved by knowing how to find the points of extremum function. In fact, they are much more. And such knowledge opens unlimited possibilities to human civilization.

In optimization tasks, it becomes necessary to find extremes functions of two or more variables provided that there is a link between the variables of this connection given by the equation . In this case, they say what to find conditional extremum .

In order to find a conditional extremum to find private derivatives and decide systems of equations There is an algorithm for finding a conditional extremum from three steps, which now and look at the example, and the geometric meaning of the conditional extremum, which must reach everyone with the analysis of this very example.

So, the algorithm that we will analyze on the example of the most common task is to find the conditional extremum function of two variables. .

Step 1. Introduced lagrange function

where the first term is the original function itself, and the second term with the minus sign is the left part of the equation of the communication condition, multiplied by (Lambda) - Lagrange multiplier.

Example 1.To find conditional extremums The functions of two variables expressing the area of \u200b\u200bthe rectangle through it x. and y. Provided that means that there is a rope that can limit this rectangle, and the length of this rope is 100.

Step 1. Decision. We present the equation of communication conditions to the desired view with zero in the right part:

.

Make up lagrange function:

Step 2. We compile a system of equations from equalities private derivatives zero and equations of communication conditions (necessary sign of the existence of a conditional extremum):

Solutions of this system of equations are points of possible conditional extremum - stationary points or, as they say, critical points.

Example 1. Step 2.

Decision.

x. and y. :

Substitute these expressions in the third equation and find the value of Lagrange multiplier:

x. and y. and find the values \u200b\u200bof the variable source function:

Received and. These values \u200b\u200bare also stationary coordinates. Thus, got a stationary point.

Step 3. Suppose that is a stationary point found in step 2. To determine whether the conditioned extremum is minimum or maximum, you need to find the second differential of the Lagrange function

and in the resulting expression, it is substantiated instead of "lambda" (Lagrange multiplier values) found in step 2.

If the value of the second differential of the Lagrange function is less than zero (), the stationary point is a maximum point, if more zero (), the stationary point is a minimum point. If the value of the second differential function of the Lagrange function is zero, additional studies are required, but such cases practically do not fall into the tasks set by students.

Coordinates of stationary points are substituted at the starting point and, thus, we finally find conditional extremums (or a minimum and maximum or something one of these extremum).

Example 1. Step 3.

Decision. We will find the second differential of the Lagrange function:

In our case, since the first and third components are zero, we will not have to substitute the Lagrange multiplier values. But you need to find relationships between differentials dX and dY. :

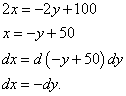
Since the values \u200b\u200bobtained are opposite by sign, we get that in any case.

Now we can find a value conditional extremum The initial function, which is the maximum:

.

This is the maximum rectangle area given by the initial function, which can be limited to the rope, the length of which is 100.

Example 2.To find conditional extremums

Step 1. Make up lagrange function:

Step 2. We will find private derivatives of Lagrange functions and make up of their equalities zero and equations of the communication condition of the system of equations:

From the first and second equations will express respectively x. and y. :

We substitute these expressions in the third equation and find the Lagrange multiplier values:

Now we will now substitute the value of Lagrange multiplier in expressions for x. and y. and find the values \u200b\u200bof the variable source function at two values \u200b\u200bof the Lagrange multiplier:

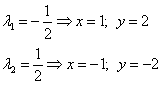
These values \u200b\u200bof the ICA and the game are the coordinates of two stationary points. Thus, received stationary points .

Step 3. Find private derivatives of the second order Lagrange function:

Find the second differential function of Lagrange by the formula

:

Received a value less zero, therefore, point - point conditional maximum:

.

I will install a sign of the second differential of the Lagrange function when the Lagrange multiplier value:

Received value, more zero, therefore, point - point conditional minimum:

.

In this way, conditional extremums The specified function is found.

Example 3.To find conditional extremums The functions of two variables provided.

Step 1. Make up lagrange function:

Step 2. We will find private derivatives of Lagrange functions and make up of their equalities zero and equations of the communication condition of the system of equations:

From the first and second equations will express respectively x. and y. :

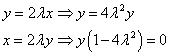
We obtain that, however, the substitution of these values \u200b\u200bof the variables in the third equation of the system does not give faithful equality. Therefore, we believe that in fact the second plant of equality is zero :. From here we get

We are looking for coordinates of stationary points with the value of the Lagrange multiplier. Then, from expressions for the ICA and the game, it follows from the system of equations that. From the third equation of the system we get.