Teise järgu read. Ellips ja selle kanooniline võrrand. Ring. Teist järku rea loeng Esimest järku rea võrrand
Ümbermõõdu järgi nimetatakse kõigi ühest antud punktist võrdsel kaugusel asuvate tasandi punktide hulgaks, nn ringi keskpunkt. Nimetatakse kaugust ringi keskpunktist ringi suvalise punktini ... ringi raadius.
- ringi kanooniline võrrand (16) - ringi keskpunkt.
Kui ringi keskpunkt asub algpunktis, siis ringjoone võrrand (16 .)
Ellips nimetatakse tasandi kõigi punktide hulgaks, mille kauguste summa selle tasandi kahest etteantud punktist (nn. trikid sellest ellipsist) on konstantne väärtus.
 B (0; b) M (x, y)
B (0; b) M (x, y)
r 1 r 2 r 1 + r 2 = 2a
(-а; 0) F 1 (-c; 0) 0 F 2 (c; 0) (а; 0) X
Lühidalt tähistame a 2 -b 2 = c 2 (*), siis ellipsi võrrandit: (17)
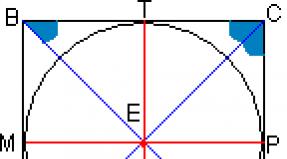
Kui paneme y = 0, siis selgub, ja kui paneme x = 0, siis selgub; seega ja on ellipsi pooltelgede pikkused - suur() ja väike(). Lisaks ei saa vasakpoolses servas olla rohkem kui üks termin ja seetõttu asub kogu ellips ristküliku sees. Punkte A, B, C, D, kus ellips lõikub oma sümmeetriatelgedega, nimetatakse ellipsi tipud.
Suhtumine ![]() nimetatakse ellipsi ekstsentrilisuseks.
nimetatakse ellipsi ekstsentrilisuseks.
Hüperbool nimetatakse tasandi kõigi punktide hulgaks, mille kauguste vahe mooduliks selle tasandi kahest etteantud punktist (nn. trikid sellest hüperboolist) on konstantne väärtus. Koldetevahelise kauguse keskpunktiks nimetatakse hüperbooli keskpunkt.


r 2 r 1 –r 2 = 2a
F1 (-c; 0) 0 F2 (c; 0) x
Tähistame 2 -c 2 = -b 2 (**), hüperbooli võrrandit: (18)
Sellest võrrandist on näha, et hüperboolil on ka kaks sümmeetriatelge (peatelg), samuti sümmeetriakese (hüperbooli keskpunkt).
Suhtumine ![]() nimetatakse hüperbooli ekstsentrilisuseks.
nimetatakse hüperbooli ekstsentrilisuseks.
Kui paneme y = 0, siis selgub, ja kui paneme x = 0, siis selgub.
Nii et Härg telg lõikab hüperbooli kahes punktis (hüperbooli tipud), see on - tegelik telg; Oy telg ei ristu hüperbooliga – see on " kujuteldav telg. »Nimetatakse mis tahes lõiku, mis ühendab hüperbooli kahte punkti, kui see läbib keskpunkti hüperbooli läbimõõt.
Nimetatakse sirgjoont, millele kõverjoon läheneb meelevaldselt lähedale, kuid ei ristu seda kunagi kõvera asümptoot. Hüperboolil on kaks asümptooti. Nende võrrandid on järgmised: (19)
Parabool tasandi kõigi punktide hulka nimetatakse kauguseks, millest igaühest antud punktini (nn keskenduda) on võrdne kaugusega etteantud sirgest (nn direktor).
- parabooli parameeter.
Paraboolil on üks sümmeetriatelg. Parabooli ja sümmeetriatelje lõikepunkti nimetatakse parabooli tipp.
Algpunktis tipuga parabooli kanooniline võrrand, mille sümmeetriatelg on Ox-telg ja harud on suunatud paremale, on kujul (20)
Tema direktori võrrand:
Algpunktis tipuga parabooli kanooniline võrrand, mille sümmeetriatelg on härja telg ja oksad on suunatud vasakule, on kujul ![]() (20 ,)
(20 ,)
Tema direktori võrrand:
Parabooli kanooniline võrrand, mille alguspunktis on tipp, mille sümmeetriatelg on Oy telg ja ülespoole suunatud harud, on kujul ![]() (20 ,)
(20 ,)
Tema direktori võrrand:
Parabooli kanooniline võrrand, mille alguspunktis on tipp, mille sümmeetriatelg on Oy telg ja allapoole suunatud harud on kujul ![]() (20 ,)
(20 ,)
Tema direktori võrrand:

 y a
y a
F 0 p / 2 x -p / 2 0 x
 a a
a a
 p / 2
p / 2
-P / 2
Teema 2.1. 7. loeng 10. tund
Teema: Ühe sõltumatu muutuja funktsioonid, nende graafikud.
Funktsiooni kontseptsioon
Üks matemaatilisi põhimõisteid on funktsiooni mõiste. Funktsiooni mõiste on seotud kahe hulga elementide vahelise seose (seose) loomisega.
Olgu antud kaks mittetühja hulka X ja Y. Vastavust ƒ, mis omistab igale elemendile xÎ X ühe ja ainult ühe elemendi yÎ Y, nimetatakse funktsiooniks ja kirjutatakse y = ƒ (x), xÎ X või ƒ : X → Y. Nad ütlevad ka, et funktsioon ƒ kaardistab hulga X hulgaga Y.

Näiteks joonisel 98 a ja b näidatud vastavused ƒ ja g on funktsioonid, kuid joonisel 98 c ja d mitte. Juhul c – mitte iga element xÎX ei vasta elemendile yÎY. Juhul r, ei ole unikaalsustingimus täidetud.
Hulka X nimetatakse funktsiooni ƒ domeeniks ja seda tähistatakse D (f). Kogu yÎY kogumit nimetatakse funktsiooni ƒ väärtuste kogumiks ja seda tähistatakse tähega E (ƒ).
Numbrilised funktsioonid. Funktsioonide graafik. Funktsioonide seadistamise meetodid
Olgu antud funktsioon ƒ: X → Y.
Kui hulkade X ja Y elemendid on reaalarvud (st XÌ R ja YÌ R), siis funktsiooni ƒ nimetatakse arvfunktsiooniks. Järgnevalt uurime (reeglina) arvulisi funktsioone, lühiduse huvides nimetame neid lihtsalt funktsioonideks ja kirjutame y = ƒ (x).
Muutujat x nimetatakse sel juhul argumendiks või sõltumatuks muutujaks ja y-d funktsiooniks või sõltuvaks muutujaks (x-st). Suurused x ja y ise on funktsionaalses seoses. Mõnikord kirjutatakse y funktsionaalne sõltuvus x-st kujul y = y (x), ilma sõltuvuse tähistamiseks uut tähte (ƒ) sisestamata.
Privaatne väärtus funktsioonid ƒ (x) x = a korral kirjutatakse järgmiselt: ƒ (a). Näiteks kui ƒ (x) = 2x 2 -3, siis ƒ (0) = - 3, ƒ (2) = 5.
Funktsioonide graafik y = (x) nimetatakse Oxy tasandi kõigi punktide hulgaks, millest igaühe jaoks on x argumendi väärtus ja y on funktsiooni vastav väärtus.
Näiteks funktsiooni y = √ (1-x 2) graafik on raadiusega R = 1 ülemine poolring, mille keskpunkt on O (0; 0) (vt joonis 99).

Funktsiooni y = ƒ (x) defineerimiseks on vaja näidata reegel, mis võimaldab x teades leida y vastava väärtuse.
Enamasti on funktsiooni määratlemiseks kolm võimalust: analüütiline, tabel, graafiline.
Analüütiline viis: funktsioon on määratud ühe või mitme valemi või võrrandina.

Kui funktsiooni y = ƒ (x) definitsioonipiirkonda ei näidata, siis eeldatakse, et see langeb kokku argumendi kõigi väärtuste hulgaga, mille jaoks vastav valem on mõttekas. Seega on funktsiooni y = √ (1-x2) määratluspiirkond segment [-1; 1].
Funktsiooni analüütiline defineerimise viis on kõige täiuslikum, kuna sellega kaasnevad matemaatilise analüüsi meetodid, mis võimaldavad funktsiooni y = ƒ (x) täielikult uurida.
Graafiline viis: määratakse funktsiooni graafik.
Sageli koostatakse graafikud automaatselt salvestitega või kuvatakse kuvaril. Funktsiooni y väärtused, mis vastavad argumendi x ühele või teisele väärtusele, leitakse otse sellelt graafikult.
Graafilise ülesande eeliseks on selgus, miinuseks ebatäpsus.
Tabeliviis: funktsioon määratakse argumentide väärtuste ja vastavate funktsiooniväärtuste tabeli abil. Näiteks tuntud trigonomeetriliste funktsioonide väärtuste tabelid, logaritmilised tabelid.
Praktikas on sageli vaja kasutada eksperimentaalselt või vaatluste tulemusena saadud funktsiooni väärtuste tabeleid.
Vaatleme sirgeid, mis on määratletud teise astme võrrandiga praeguste koordinaatide suhtes
Võrrandi kordajad on reaalarvud, kuid vähemalt üks arvudest A, B või C erineb 0-st. Selliseid jooni nimetatakse teist järku joonteks (kõverateks). Allpool näitame, et võrrand (1) defineerib tasapinnal ringi ellipsi, hüperbooli või parabooli.
Ring
Lihtsaim teist järku kõver on ring. Tuletame meelde, et punktis M 0 tsentreeritud ring raadiusega R on tasandi punktide M hulk, mis vastab tingimusele MM 0 = R. Olgu Oxy süsteemi punkti M 0 koordinaadid x 0, y 0 ja M (x, y) on ringjoone suvaline punkt. Siis kas
-ringi kanooniline võrrand ... Seadistades x 0 = y 0 = 0 saame x 2 + y 2 = R 2
näitame, et ringi võrrandi saab kirjutada teise astme üldvõrrandi (1) kujul. Selleks paneme ringvõrrandi parema külje ruudu ruutu ja saame:
Selle võrrandi vastamiseks (1) on vajalik, et:
1) koefitsient B = 0,
2). Siis saame: (2)
Viimast võrrandit nimetatakse ringi üldvõrrand ... Jagades võrrandi mõlemad pooled A ≠ 0-ga ja liites x-i ja y-d sisaldavad terminid täisruudule, saame:
![]() (2)
(2)
Võrreldes seda võrrandit ringi kanoonilise võrrandiga, saame, et võrrand (2) on tegelikult ringi võrrand, kui:
1) A = C, 2) B = 0, 3) D 2 + E 2 -4AF> 0.
Kui need tingimused on täidetud, asub ringi keskpunkt punktis O ja selle raadius ![]() .
.
Ellips
|
|
|
|
Olgu M (x, y) ellipsi suvaline punkt, siis vastavalt ellipsi definitsioonile on MF 1 + MF 2 = 2, mis on
See on ellipsi võrrand. Saate selle lihtsamaks vormiks teisendada järgmiselt.
Ruudukujuline:
![]()
ruut
Kuna siis 2 -c 2> 0 pane 2 -c 2 = b 2
Siis saab viimane võrrand järgmise kuju:
![]()
on ellipsi võrrand kanoonilisel kujul.
Ellipsi kuju sõltub suhtest: kui b =, muutub ellips ringiks. Võrrand võtab kuju. Suhet kasutatakse sageli ellipsi tunnusena. Seda väärtust nimetatakse ellipsi ekstsentrilisuseks ja 0< <1 так как 0 Ellipsi kuju uurimine. 1) ellipsi võrrand sisaldab x ja y, vaid paarisastmes, mistõttu on ellips sümmeetriline telgede Ox ja Oy suhtes, samuti punkti O (0,0) suhtes, mida nimetatakse telgede keskpunktiks. ellips. 2) leida ellipsi lõikepunktid koordinaattelgedega. Kui panna y = 0, leiame A 1 (, 0) ja A 2 (-, 0), kus ellips lõikub punktiga Ox. Kui panna x = 0, leiame B 1 (0, b) ja B 2 (0, -b). Punkte A 1, A 2, B 1, B 2 nimetatakse ellipsi tippudeks. Lõike A 1 A 2 ja B 1 B 2 ning nende pikkusi 2 ja 2b nimetatakse vastavalt ellipsi suur- ja väiketeljeks. Arvud ja b on vastavalt suured ja väiksemad poolteljed. 4) Ellipsi võrrandis on mittenegatiivsete liikmete summa võrdne ühega. Seega, kui üks liige suureneb, väheneb teine, see tähendab, kui | x | suureneb, siis | y | - väheneb ja vastupidi. Kõigest öeldust järeldub, et ellipsil on joonisel 2 näidatud kuju. (ovaalne suletud kõver). Laadige alla saidist Depositfiles Loeng number 9. Teema 3: teist järku read Olgu mõnes DSC-s antud teise astme võrrandiga defineeritud sirge kus koefitsiendid Võib juhtuda, et punkte polegi Vaatleme võrrandi (1) kolme olulist erijuhtu. 3.1. Ellips Ellips on defineeritud võrrandiga Koefitsiendid a ja b
nimetatakse vastavalt suur- ja väikepooltelgedeks ning võrrandit (2) - kanooniline ellipsi võrrand. Panime punktide asukoht, kauguste summa fookustest on konstantne väärtus, mis on võrdne 2a.
b
M
K
—
aF 1 O F
2 a
x
—
b
Näitame seda. Olgu punkt Avaldist (3) saab esitada kui ja avaldise mõlemad pooled ruudukujuliseks Sellest saame Teeme selle avaldise ruudu uuesti ja kasutame seost Avaldise (4) mõlema osa jagamine arvuga Uurime võrrandit (2). Kui võrrand asendatakse, siis võrrand (2) ei muutu. See tähendab, et ellips on sümmeetriline koordinaattelgede suhtes. Seetõttu käsitleme üksikasjalikult esimeses kvartalis asuvat ellipsi osa. See määratakse võrrandiga Suhtumine Otsene Kehtib järgmine direktorite omadus:
Ellipsi punktide fookuse ja suuna kauguste suhe on konstantne väärtus, mis on võrdne ekstsentrilisusega, s.o. Tõestus sarnaneb võrdsusega (3). Märkus 1. Ring 3.2. Hüperbool Kanoonilisel hüperbooli võrrandil on vorm need. võrrandisse (1) tuleb panna Koefitsiendid a ja b
nimetatakse vastavalt reaalseks ja imaginaarseks poolteljeks. Panek punktide asukoht, vahekauguste erinevus fookustest absoluutväärtuses on 2a, st. TO
M F
1
—a
O aF
2
NS Tõestus on sarnane ellipsi omaga. Hüperbooli võrrandi abil järeldame ka, et selle graafik on sümmeetriline koordinaatsüsteemi telgede suhtes. Hüperbooli esimesel veerandil paikneval osal on võrrand Punktid Suhet nimetatakseekstsentrilisushüperbool. Hüperbooli jaoks Sirgeid jooni nimetatakse lavastajad hüperbool. Hüperbooli otsejoone puhul on omadus sarnane ellipsi suuna omaga. Näide. Leidke ellipsi võrrand, mille tipud asuvad hüperbooli tippudes ja fookused Tingimuste järgi Lõpuks saame 10.3. Parabool Parabool on defineeritud kanoonilise võrrandiga TO fookusparameeter. M Märkus O-telje kohta NSpunkt hüperbool. 1. peatükk TEINE TELLIMUSED LENNUKIS 1. Ellipsi, hüperbooli, parabooli määratlus. Ellips on tasandi kõigi punktide kogum, mille puhul kahe antud punkti F 1 ja F kauguste summa on konstantne väärtus a, mis ületab kaugust F 1 ja vahel. M (, x) F 1 О F x Joon. Punkte F 1 ja F nimetatakse ellipsi fookuspunktideks ning nendevaheline kaugus FF 1 on fookuskaugus, mida tähistatakse c. Olgu punkt M ellipsi alla kuuluv. Lõike F1 M ja F M nimetatakse punkti M fookusraadiusteks. Olgu F1F = c. Definitsiooni järgi on a> c. Vaatleme ristkülikukujulist Descartes'i koordinaatsüsteemi Ox, milles fookused F 1 ja F paiknevad abstsissteljel sümmeetriliselt alguspunkti suhtes. Selles koordinaatsüsteemis kirjeldatakse ellipsi kanoonilise võrrandiga: x + = 1, a b 1 2. kus b = a c Parameetreid a ja b nimetatakse vastavalt ellipsi suuremaks ja väiksemaks poolteljeks. Ellipsi ekstsentrilisus on arv ε, mis võrdub poole fookuskauguse c suhtega poolsuurteljesse, s.o. ε =. Ellipsi a ekstsentrilisus rahuldab võrratusi 0 ε< 1. Случай c = 0 соответствует окружности, эксцентриситет окружности равен нулю. Фокальные радиусы точки M(x,) эллипса могут быть найдены по формулам r 1 = a ε x, r = a+ ε x. Нормальное уравнение окружности имеет вид (x c) + (d) = R. Определение. Гиперболой называется множество всех точек плоскости, для которых абсолютная величина разности расстояний до данных точек F 1 и F есть величина постоянная, равная a. Точки F 1 и F называются фокусами гиперболы, а расстояние между ними фокальным расстоянием, которое обозначается c. Отрезки F1 M и F M называются фокальными радиусами точки M (x,) гиперболы. Рассмотрим прямоугольную декартову систему координат Ox, в которой фокусы F 1 и F расположены на оси абсцисс симметрично относительно начала координат. M (x,) F 1 F x Рис. 3 3 Kanoonilise hüperbooli võrrandi vorm on x a = b 1 ,. kus b = c a Arve a ja b nimetatakse vastavalt hüperbooli reaal- ja imaginaarseteks pooltelgedeks. Ebavõrdsusega määratletud piirkonnas ei ole hüperbooli. x a b Definitsioon. Hüperbooli asümptoodid on sirged, b b, mis on antud võrranditega = x, = x. a a Hüperbooli punkti M (x,) fookusraadiused on leitavad valemitega r 1 = ε x a, r = ε x + a. Hüperbooli ekstsentrilisus, nagu ka ellipsi puhul, määratakse valemiga ε =. Lihtne on kontrollida, kas ebavõrdsus ε a> 1 vastab hüperbooli ekstsentrilisusele. Definitsioon. Parabool on tasandi kõigi punktide hulk, mille kaugus antud punktist F on võrdne kaugusega antud sirgest d, mis ei läbi punkti F. Punkti F nimetatakse parabooli fookuseks ja sirget d nimetatakse otsejooneks. Kaugust fookusest otsejooneni nimetatakse parabooli parameetriks ja seda tähistatakse p. d M (x,) F x Joon. 4 3 4 Valime lõigu FD keskel asuva Descartes'i koordinaatsüsteemi algpunkti O, mis on punktist F sirgele d langetatud risti. Selles koordinaatsüsteemis on fookuse F koordinaadid F p p; 0 ja suund d on antud võrrandiga x + = 0. Parabooli kanooniline võrrand on: = px. Parabool on sümmeetriline OF-telje suhtes, mida nimetatakse parabooli teljeks. Selle telje ja parabooli lõikepunkti O punkti nimetatakse parabooli tipuks. Punkti M fookusraadius (x,) s.o. selle p kaugus fookuseni leitakse valemiga r = x +. 10B .. Teist järku sirge üldvõrrand Teist järku sirge on punktide hulk tasapinnal, mille koordinaadid x ja mis vastavad võrrandile ax + ax + a + ax + a + a = 0, 11 1 kus a11 , a1, a, a10, a0, a00 mõned reaalarvud ja a, a, a ei ole samal ajal võrdsed nulliga. Seda võrrandit nimetatakse teist järku kõvera üldvõrrandiks ja selle saab kirjutada ka vektorkujul rr rr (Ax, x) + (b, x) + a = 0, kus 00 a11 a1 rr A =, a1 ab = (a10; a0) , x = (x;). T Kuna A = A, siis A on ruutkujuga maatriks r r r f (x) = (Ax, x) = a x + a x + a Ellips, hüperbool ja parabool on tasandi teist järku kõverate näited. Lisaks nendele kõveratele on ka teist tüüpi teist järku kõveraid, mis on seotud x joontega. Näiteks võrrand = 0, kus a 0, b 0, a b 4 5 määratleb tasapinnal lõikuvate sirgete paari. Koordinaatsüsteeme, milles kõvera võrrand võtab kõige lihtsama kuju, nimetatakse kanoonilisteks. Kasutades teisenduste kompositsiooni: telgede pööramine läbi nurga α, lähtepunkti paralleelne translatsioon punkti (x0; 0) ja peegeldus ümber abstsisstelje, taandatakse teist järku kõvera võrrand ühele kanoonilisest. võrrandid, millest peamised olid loetletud eespool. 11BNäited 1. Koostage kanooniline võrrand ellipsile, mille keskpunkt on alguspunktis ja fookused asuvad abstsissteljel, kui on teada, et selle ekstsentrilisus ε = ja punkt N (3;) asub 3. ellipsil. x a b Ellipsi võrrand: + = 1. Meil on see =. a b a 3 9 Sellest arvutame, et a = b. Asendades võrrandisse punkti N (3;) koordinaadid, saame + = 1 ja siis b = 9 ja a b 81 a = = 16 ,. Järelikult on ellipsi kanooniline võrrand 5 x + = 1. 16, 9. Kirjutage hüperbooli kanooniline võrrand, mille keskpunkt on alguspunktis ja fookused asuvad abstsissil, kui punkt M 1 (5; 3) hüperbool ja ekstsentrilisus ε = on antud. x Hüperbooli kanooniline võrrand = 1. Võrdusest a b a + b = saame b = a 5 9. Seega = 1 ja a = 16. Seetõttu on ellipsi kanooniline võrrand = a a a x 16 5 6 3. Leidke punktid paraboolilt = 10x, mille fookusraadius on 1,5. Pange tähele, et parabool asub paremal pooltasandil. Kui M (x; asub paraboolil, siis x 0. Parameeter p = 5. Olgu (;)) M x parabooli vajalik punkt, F fookus, () suund. Siis F, 5; 0, d: x =, 5. Kuna FM = ρ (M, d), siis x +, 5 = 1,5, 10 Vastus: () 1 10; 10 x =, = 100, = ± 10. Seega saime kaks punkti. M 10; 10 M, () 4. Leia võrrandiga x = 1 antud hüperbooli paremal harul punkt, mille kaugus parempoolsest fookusest on 16 9 kaks korda väiksem kui selle kaugus vasakpoolsest fookusest. Hüperbooli parempoolse haru jaoks määratakse fookusraadiused valemitega r 1 = ε x a ja r = ε x + a. Seetõttu saame võrrandi ε x + a = (ε x a). Antud hüperbooli korral a = 4, 5, c = 5 ja ε =. Seega x = 9,6. Seega on = ± x 16 = ± d. Vastus: kaks punkti M 1 (9,6; 0,6 119), (9,6; 0,6 119) M. 5. Leidke sirge võrrand, mille mis tahes punkti kauguse suhe punkt F (3; 0) kauguseni sirgest 1 x 8 = 0 on võrdne ε =. Määrake rea nimi ja selle parameetrid. M x; soovitud sirgel on võrdus tõene: Suvalise punkti () korral FM (x 3) + 1 = =. ρ (Ml) x 8 6 7 Seega on meil [(x 3) +] = (x 8). Sulgusid laiendades ja termineid ümber paigutades saame (x +) + = 50, s.o. (x +) + = Vastus: vajalik sirge on ellips, mille keskpunkt on punktis ja poolteljed a = 5 ja b = Leia hüperbooli võrrand Koordinaatide vanad koordinaadid O () x; 0; ;,;. C (; 0) = 8 uues süsteemis (x;) ja uued (zt;) on seotud maatriksvõrdusega 1 1 x z 1 z + t = 1 1 t = z t. Seega võrrand x = 8 z + t z t = 8, zt = 4. Vastus: zt = 4. γ: 4x 4x + 8x + 4+ 3 = 0 kuni cano- 7. Viige kõver kordumatule kujule. uutes koordinaatides on kujund Vaatleme ruutkuju () q x, = 4x 4x +. Vormi q maatriksil on omaväärtused 5 ja 0 ning vastavad ortonormaalvektorid ja läheme üle uuele koordinaatsüsteemile: 7 8 z 1 1 x. t = 5 1 Avaldame vanad koordinaadid (x;) uutega (zt); : 1 1 z + tx 1 z = 1 t =, 1 zt tähendab, x = z + t, = z + t Asendades need avaldised kõvera γ võrrandisse, saame 0 = 4x 4x + 8x = x = z + 1 t, = 1 z + t ( ) () () () = 5z 4 5z + 3 = z 5 4 z 5 + 3 = z 5 1 z 5 3. Seega on uutes koordinaatides antud kõver γ võrrandi 1 3 γ järgi: zz =. Seadistamisel = z, x = t, saame γ: =, 1, millest leiame kõvera γ kanoonilise võrrandi: = 0 kanoonilistes koordinaatides = 5 x 1 1 x Pange tähele, et kõver γ on paralleelsete sirgete paar. 1B Majandus- ja finantsprobleemide lisad 8. Las Anyal, Borissil ja Dmitril on puuviljade ostmiseks igaühel 150 rubla. Teadaolevalt maksab 1 kg pirne 15 rahaühikut ja 1 kg õunu 10 rahaühikut. Lisaks on kõik kolm 8 9-l on oma kasulik funktsioon, mida ta soovib ostmisel maksimeerida. Ostetakse x1 kg pirne ja x kg õunu. Need kasulikud funktsioonid on järgmised: u = x + x Ani jaoks, 1 A 1 x u B = + x Borisi jaoks ja ud = x1 x Dmitri jaoks. Ani, Borisi ja Dmitri jaoks on vaja leida ostuplaan (x1, x), milles nad pakuvad maksimaalselt oma kasulikku funktsiooni. x Joon. 5 Vaadeldavat ülesannet saab lahendada geomeetriliselt. Selle probleemi lahendamiseks tuleks kasutusele võtta tasapinnalise joone mõiste. x x 1 Joon. 6 Funktsiooni z = f (x,) tasemejoon on kõigi tasandi punktide hulk, millel funktsioon säilitab konstantse väärtuse, mis on võrdne h-ga. x 9 10 Sel juhul kasutab lahendus ka tasandi geomeetriliste domeenide algmõisteid, mis on määratud lineaarsete võrratustega (vt alajaotis 1.4). x x 1 Joon. 7 Funktsioonide ua, u B ja u D tasemejooned tähistavad vastavalt Ani, Borisi ja Dmitri sirgeid, ellipse ja hüperboole. Ülesande mõttes eeldame, et x1 0, x 0. Teisest küljest kirjutatakse eelarvepiiranguks ebavõrdsus 15x1 + 10x 150. Jagades viimase võrratuse 10-ga, saame 3x1 + x 30 või + 1. On lihtne näha, et x1 x on selle võrratuse lahendite piirkond koos mittenegatiivsuse tingimustega on kolmnurk, mis on piiratud sirgetega x1 = 0, x = 0 ja 3x1 + x = 11 X * X * Joon. 8 Joon. 9 Geomeetriliste mustrite põhjal on nüüd lihtne kindlaks teha, et uamax = ua (0,15) = 15, ubmax = ub (0,15) = 5 ja udmax = ud (Q). Eelarvekolmnurga külje tasandi hüperbooli puutepunkti Q koordinaadid tuleb juba analüütiliselt välja arvutada. Selleks pange tähele, et punkt Q vastab kolmele võrrandile: xx 1 = h, 3x1 + x = 30, h 3 x "= =. X1 X * Joon. 12 Elimineerides võrranditest h, saame punkti Q = (x, x) = (5; 7.5) koordinaadid. 1 Vastus: Q = (x1, x) = (5; 7,5). 9. Ettevõtte kulude ja kasumite mittelineaarne mudel. Las ettevõte toodab kahte tüüpi, A ja B, mitmeotstarbelisi seadmeid vastavalt koguses x ja tootmisühikutes. Sel juhul väljendatakse ettevõtte aasta tulu tulufunktsiooniga Rx (,) = 4x + ja tootmiskulusid kulufunktsiooniga 1 1 Cx (,) = 7,5+ x + 4, mille ettevõte saab maksimaalne kasum. Määrake tootmisplaan (x, ) punktis 3 13 Kasumifunktsioon koostatakse tulufunktsiooni ja kulufunktsiooni vahena: 1 1 Π (x,) = R (x,) C (x,) = 4x + 7,5 x. 4 Pärast teisenduste tegemist taandatakse viimane avaldis kujule 1 1 Π (x,) = 9 (x 8) (1). 4 Kasumifunktsiooni tasemejooned on (x 8) (1) = h. 4 Iga taseme joon 0 h 9 on ellips, mille keskpunkt on alguspunktis. Saadud avaldisest on hsti nha, et kasumifunktsiooni maksimum on 9 ja saavutatakse x = 8, = 1. Vastus: x = 8, = 1. 13BEHistused ja testi ksimused.1. Kirjutage ringi normaalvõrrand. Leidke ringi keskpunkti ja raadiuse koordinaadid: a) x + + 8x 6 = 0; b) x x = 0 ... Koostage punkte M 1 (1;), M (0; 1), M 3 (3; 0) .. 3 läbiva ringjoone võrrand. Defineeri ellips ja kirjuta selle kanooniline võrrand. Kirjutage ellipsi kanooniline võrrand, kui 1 selle ekstsentrilisus on ε = ja poolsuurtelg on võrdne Koostage võrrand ellipsist, mille fookused asuvad ordinaatteljel sümmeetriliselt alguspunkti suhtes, teades lisaks , et selle fookuste vaheline kaugus on c = 4 ja ekstsentrilisus ε = Määrake ellipsi ekstsentrilisus. Leidke ellipsi ekstsentrilisus, kui selle peatelg on neli korda väiksem kui väiketelg. 33 14 .6. Defineerige hüperbool ja kirjutage selle kanooniline võrrand. Läbi punkti M (0; 0,5) ja hüperbooli parempoolse tipu tõmmatakse sirgjoon, mis on antud võrrandiga = 1. Leidke sirge ja hüperbooli teise lõikepunkti koordinaadid. Määrake hüperbooli ekstsentrilisus. Kirjutage selle kanooniline võrrand, kui a = 1, b = 5. Mis on selle hüperbooli ekstsentrilisus? .8. Kirjutage selle kanoonilise võrrandiga antud hüperbooli asümptootide võrrandid. Koostage hüperbooli 3 võrrand, kui selle asümptoodid on antud võrranditega = ± x ja hüperbool 5 läbib punkti M (10; 3 3) .. 9. Defineerige parabool ja kirjutage selle kanooniline võrrand. Kirjutage parabooli kanooniline võrrand, kui abstsisstelg on selle sümmeetriatelg, selle tipp asub lähtepunktis ja parabooli hõlju pikkus risti teljega on 8 ning selle kõõlu kaugus tipust on Paraboolil = 1x Leia punkt, mille fookusraadius on Propositsioon ja nõudlus teatud toote järele on antud funktsioonidega p = 4q 1, p = +. Leidke turu tasakaalupunkt. 1 q Loo graafikud ... 1. Andrey, Katya ja Nikolay ostavad apelsine ja banaane. Osta x1 kg apelsine ja x kg banaane. Igal neist kolmest on oma kasulik funktsioon, mis näitab, kui kasulikuks ta oma ostu peab. Need kasulikud funktsioonid on järgmised: u = x + x Andrei jaoks, 1 4 A 4 1 u K = x + x Katja jaoks ja un = x1 x Nikolai jaoks. a) Joonistage kasuliku funktsiooni taseme read taseme h = 1, 3 väärtuste jaoks. b) Järjestage iga jaoks ostueelistuse järjekorras rrr r = (4,1), s = ( 3,8), t = (1,1). 34 Analüütilise geomeetria moodul. Analüütiline geomeetria tasapinnal ja ruumis Loeng 7 Kokkuvõte Teist järku jooned tasapinnal: ellips, hüperbool, parabool. Definitsioon, üldised omadused. LOENG N15. Teise järgu kõverad. 1.Ringjoon ... 1.Ellips ... 1 3.Hüperbool .... 4.Parabool .... 4 1.Ring Teist järku kõver on sirge, mis on määratletud teise astme võrrandiga 8 Teist järku kõverad 81 Ringjoon Tasapinna punktide kogum, mis on ühest punktist võrdsel kaugusel, mida nimetatakse keskpunktiks, kaugusel, mida nimetatakse raadiuseks ja mida nimetatakse ringiks. Olgu ringjoone keskpunkt 13. loeng Teema: Teist järku kõverad Teist järku kõverad tasapinnal: ellips, hüperbool, parabool. Teist järku kõverate võrrandite tuletamine nende geomeetriliste omaduste põhjal. Uurides ellipsi kuju, LOENG Hüperbooli teist järku sirged Näitena leiame võrrandid, mis defineerivad ringi, parabooli, ellipsi ja ringi Ring on punktide kogum tasapinnal, mis on etteantust võrdsel kaugusel. Teist järku kõverad Ringellips Hüperbool Parabool Olgu antud tasapinnal ristkülikukujuline Descartes'i koordinaatsüsteem. Teist järku kõver on punktide kogum, mille koordinaadid vastavad Sirge ja tasapind ruumis Lineaaralgebra (loeng 11) 24.11.2012 2/37 Sirge ja tasapind ruumis Kahe punkti vaheline kaugus M 1 (x 1, y 1, z 1) ja M 2 (x 2, y) 2, z 2) Vene Föderatsiooni Haridus- ja Teadusministeerium Jaroslavli Riiklik Ülikool oma nime saanud P.G.Demidova Algebra ja matemaatilise loogika osakond II järgu kõverad I osa Metoodilised juhised 3. Hüperbool ja selle omadused Definitsioon 3 .. Hüperbool on kõver, mis on defineeritud mõnes ristkülikukujulises Descartes'i koordinaatsüsteemis võrrandiga 0. (3.) ja Võrdsust (3.) nimetatakse kanooniliseks võrrandiks Praktiline tund 1 Teema: Hüperbooli plaan 1 Hüperbooli definitsioon ja kanooniline võrrand Hüperbooli geomeetrilised omadused Hüperbooli ja selle keskpunkti läbiva sirge vastastikune asend Asümptoodid Loengukonspekt 13 ELLIPS, HÜPERBALL JA PARABOOL 0. Loengukava Loengu Ellips, Hüperbool ja Parabool. 1. Ellips. 1.1. Ellipsi määratlus; 1.2. Kanoonilise koordinaatsüsteemi määramine; 1.3. Võrrandi tuletamine PARABOOL HÜPERBALLELLIPSI MOODUL Praktiline tund Teema: Ellipsi plaan Ellipsi definitsioon ja kanooniline võrrand Ellipsi geomeetrilised omadused Ekstsentrilisus Ellipsi kuju sõltuvus ekstsentrilisusest TEINE PROBLEEM 1. Sirge joon tasapinnal. 1. Kaks sirget on antud vektorvõrranditega (, rn) = D ja r = r + a, ja (an,) 0. Leidke sirgete lõikepunkti raadiusvektor. 0 t. Antud punkt М 0 raadiusvektoriga Teise järgu kõverad. Definitsioon: Teist järku kõvera joon) on tasandi punktide hulk (M), mille ristkoordinaadid X, Y) vastavad teise astme algebralisele võrrandile :, ALGEBRAALISED SIRGED TASAKONDUL .. ESIMESE JÄRKU SIRGED (LINEAARID TASANDIL ... TASANDI LINEAARIDE PÕHILIIGID Antud sirgega risti olevat nullist erinevat vektorit n nimetatakse normaalväärtuseks Ellips ja selle omadused Definitsioon .. Ellips on teist järku kõver, mis on defineeritud mõnes ristkülikukujulises Descartes'i koordinaatsüsteemis võrrandiga b, b 0. (.) Võrdsust (.) nimetatakse kanooniliseks 0,5 setgray0 0,5 setgray1 1 Loeng 9 ELLIPS, HÜPERBALL JA PARABOOL 1. Ellipsi kanooniline võrrand Definitsioon 1. Ellips on punktide M asukoht tasapinnal, iga punkti kauguste summa. ANALÜÜTILISE GEOMEETIA ÕPPEKUNNI ELEMENTID KOLMEMÕÕTELISES RUUMIS Kirjutage tasapinna vektorvõrrand ja selgitage selles võrrandis sisalduvate suuruste tähendust Kirjutage tasandi üldvõrrand. 12. tund Ellips, hüperbool ja parabool. Kanoonilised võrrandid. Ellips on punktide M asukoht tasapinnal, mille puhul kahe fikseeritud punkti F 1 ja F 2 kauguste summa, nn. LINEAARALGEBRA Loeng Teist järku kõverate võrrandid Ringjoone definitsioon Ring on ühest punktist võrdsel kaugusel asuvate punktide asukoht, mida nimetatakse ringi keskpunktiks kaugusel r Uurali föderaalülikool, matemaatika ja arvutiteaduse instituut, algebra ja diskreetse matemaatika osakond Sissejuhatavad märkused Selles loengus uuritakse teist järku kolmandat kõverat, parabooli. Loeng 9.30 Peatükk Analüütiline geomeetria tasapinnal Koordinaatsüsteemid tasapinnal Ristküliku- ja polaarkoordinaadisüsteemid Koordinaatsüsteem tasapinnal on meetod, mis võimaldab määrata Vene Föderatsiooni Haridus- ja Teadusministeerium Jaroslavli Riiklik Ülikool oma nime saanud P. G. Demidova Algebra ja matemaatilise loogika osakond S. I. Yablokova Teise järgu kõverad Osa töötuba Teema ANALÜÜTILISE GEOMEETIA ELEMENDID TASAKONDIL JA RUUMIS Loeng .. Jooned tasapinnal Pl ja n. Tasapinna koordinaatide meetod .. sirge ristkoordinaatides .. Paralleelsuse ja perpendikulaarsuse tingimus Lineaaralgebra ja analüütiline geomeetria Teema: Teist järku kõverad Lektor Rožkova S.V. 01 15. Teist järku kõverad Teist järku kõverad jagunevad 1) degenereerunud ja) mitte-mandunud Degenereerunud. Loeng 11 1. KITSENEVAD LÕIKUD 1.1. Definitsioon. Vaatleme parempoolse ringkoonuse lõiku selle koonuse generatriksiga risti oleva tasapinnaga. Nurga α erinevate väärtuste jaoks aksiaalses tipus 9. loeng 1. KITSENEVAD LÕIKUD 1.1. Definitsioon. Vaatleme parempoolse ringkoonuse lõiku selle koonuse generatriksiga risti oleva tasapinnaga. Nurga α erinevate väärtuste jaoks aksiaalses tipus Uurali föderaalülikool, matemaatika ja arvutiteaduse instituut, algebra ja diskreetse matemaatika osakond Sissejuhatavad märkused Selles loengus uuritakse teist teist järku hüperboolikõverat. Praktiline tund 14 Teema: Parabooli plaan 1. Parabooli definitsioon ja kanooniline võrrand .. Parabooli geomeetrilised omadused. Parabooli ja selle keskpunkti läbiva sirge suhteline asukoht. Peamine A N A L I T I Ch E C A Z G E O M E T R I Z teise järgu kõverad SHIMANCHUK Dmitri Viktorovitš [e-postiga kaitstud] Peterburi Riikliku Ülikooli protsesside rakendusmatemaatika teaduskond Maatriksid 1 Antud maatriksid ja leia: a) A + B; b) 2B; c) B T; d) AB T; e) B T A Lahendus a) Maatriksite summa definitsiooniga b) Maatriksi korrutise definitsiooniga arvuga c) Transponeeritud maatriksi definitsiooniga VARIANT 1 1 Leidke punkte M 1 (18) ja M (1) läbiva sirge kalle k; kirjuta üles sirge võrrand parameetrilisel kujul Loo võrrandid tippudega A () kolmnurga külgede ja mediaanide jaoks. Test. Antud maatriksid A, B ja D. Leidke AB 9D, kui: 4 7 () 6 9 6 A = 3 9 7, B =, D = 3 8 3. 3 7 7 3 7 Korrutage maatriksid A 3 ja B 3. tulemuseks on C suurusega 3 3, mis koosneb elementidest 9. peatükk Kurvid tasapinnal. Teist järku kõverad 9. Põhimõisted Nad ütlevad, et kõver Γ ristkülikukujulises koordinaatsüsteemis Oxy omab võrrandit F (,) = 0, kui punkt M (x, y) kuulub selles kõverasse. Lineaaralgebra ja analüütiline geomeetria Teema: Teist järku kõverad Lektor Pakhomova E.G. 01 15. Teist järku kõverad Teist järku kõverad jagunevad 1) degenereerunud ja) mitte-mandunud Degenereerunud. Uurali föderaalülikool, matemaatika ja arvutiteaduse instituut, algebra ja diskreetse matemaatika osakond Sissejuhatavad märkused Kolmes eelnevas loengus uuriti sirgeid ja tasapindu, s.o. Peatükk 1 Teist järku kõverad ja pinnad Kõigis osades, välja arvatud 1.9, on koordinaatsüsteem ristkülikukujuline. 1.1. Teist järku kõverate ja muude kõverate võrrandite koostamine 1.p) Tõesta, et hulk ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ Moskva Riiklik Tehnikaülikool nimega N.E. Baumani põhiteaduste teaduskond matemaatilise modelleerimise osakond À.Í. Santnikov, PEATÜKK 5. ANALÜÜTILINE GEOMEETIA 5 .. Tasapinna sirge võrrand Võrrandit kujul F (x, y) 0 nimetatakse sirge võrrandiks, kui see võrrand on täidetud antud tasapinnal asuva mis tahes punkti koordinaatidega. Balakovo Inseneri- ja Tehnoloogiainstituut - föderaalse osariigi autonoomse kõrgharidusasutuse "National Research Nuclear University" MEPhI filiaal Teist järku jooned Yu. L. Kalinovskiy Kõrgema Matemaatika Osakond Ülikool "Dubna" Plaan 2 3 4 5 6 7 Teist järku read: punktide asukoht, mille ristkoordinaadid vastavad võrrandile 44. Hüperbooli definitsioon. Hüperbool on kõigi tasandi punktide hulk, mille koordinaadid sobivas koordinaatsüsteemis vastavad võrrandile 2 2 y2 = 1, (1) b2 kus, b> 0. See võrrand Lineaaralgebra ja analüütiline geomeetria Teema: Teist järku kõverad (jätk) Lektor Pakhomova E.G. 01 g 4. Ellipsi, hüperbooli ja parabooli ülddefinitsioon MÄÄRATLUS. Joone a m nimetatakse otse- 1 Loeng 1.4. Teist järku kõverad ja pinnad Kokkuvõte: Kõverate kanoonilised võrrandid on tuletatud definitsioonidest: ellips, hüperbool ja parabool. Antud on ellipsi ja hüperbooli parameetrilised võrrandid. Vene Föderatsiooni Haridus- ja Teadusministeerium Föderaalne riigieelarveline kõrgharidusasutus "Siberi Riiklik Tööstusülikool" Praktiline töö Teist järku sirgete ja kõverate võrrandite koostamine Töö eesmärk: kinnistada teist järku sirgete ja kõverate võrrandite koostamise oskust Töö sisu. Põhimõisted. B C 0 vektor Ülesanded puudutud tundide harjutamiseks Sisukord Teema: Maatriksid, tegevused nendega. Determinantide arvutamine .... 2 Teema: Pöördmaatriks. Võrrandisüsteemide lahendamine pöördmaatriksi abil. Valemid Analüütiline geomeetria 5 .. Tasapinna sirge Tasapinna sirge defineerimise erinevad viisid. Tasapinna sirge üldvõrrand. Sirge asukoht koordinaatsüsteemi suhtes. Geomeetriline tähendus VARIANT 11 1 Punkt M () on punktist N (1-1) sirgele l langetatud risti alus. Kirjutage sirge l võrrand; leida kaugus punktist N sirgeni l Kirjutage sirgete võrrandid 49. Silindrilised ja koonilised pinnad 1. Silindrilised pinnad Definitsioon. Olgu ruumis antud sirge l ja nullist erinev vektor a. Pind, mille moodustavad kõik võimalikud läbivad sirged jooned Analüütiline geomeetria Analüütiline geomeetria tasapinnal. Analüütiline geomeetria geomeetriliste ülesannete lahendamine algebra abil, mille jaoks kasutatakse koordinaatide meetodit. Koordinaatide süsteemi all lennukis 1. võimalus Ülesanne 1. Andke ellipsi geomeetriline definitsioon. Ülesanne 2. Tõesta Dandelini kuulide abil, et ellips tekib koonilise lõiguna. Ülesanne 3. Tõesta, et punktide hulk P, millest Sekaeva L.R., Tyuleneva O.N. ANALÜÜTILINE GEOMEETRIA LENNUIL Kaasan 008 0 Kaasani Riikliku Ülikooli üldmatemaatika osakond LR Sekaeva, ON Tyuleneva ANALÜÜTILINE GEOMEETIA LENKIL Vene Föderatsiooni Haridus- ja Teadusministeerium Kaasani Riikliku Arhitektuuri- ja Ehitusülikooli Kõrgema matemaatika osakond Vektor- ja lineaaralgebra elemendid. Analüütiline geomeetria. Analüütiline geomeetria tasapinnal Joonvõrrand on analüütilise geomeetria kõige olulisem mõiste. y М (x, y) 0 x Definitsioon. Oxy tasapinna sirge (kõvera) võrrand on võrrand, millele Lennuki põhiülesannete näidised Gaussi meetod Määratud lineaarvõrrandisüsteemid Lahendage Gaussi meetodil lineaarvõrrandisüsteem x 6 y 6 8, 6 x 6 y 6 Lahendage Gaussi meetodil lineaarvõrrandisüsteem 6 VARIANT 16 1 Läbi punktide M 1 (3 4) ja M (6) tõmmatakse sirge. Leidke selle sirge lõikepunktid koordinaattelgedega Koostage kolmnurga nende külgede võrrandid, mille punktid A ( 1) B (3 1) C (0 4) on Test 3 1. VARIANT. Koostage sirge võrrand, mis on risti ja läbib sirgete lõikepunkti ja .. Kirjutage üles punkte läbiva sirge võrrand ja leidke kaugus punktist ANALÜÜTILISE GEOMEETRIA ELEMENDID LENKIL. Sirge 1. Arvuta ümbermõõt kolmnurgale, mille tipud on punktid A (6; 7), B (3; 3), C (1; 5). 2. Leidke punkt, mis asub punktidest A võrdsel kaugusel (7; Analüütiline geomeetria Moodul 1 Maatriksalgebra Vektoralgebra Tekst 5 (iseseisev uuring) Annotatsioon Descartes'i ristkülikukujuline koordinaatsüsteem tasapinnal ja ruumis Kauguse valemid Vene Föderatsiooni Haridusministeerium Rostovi Riikliku Ülikooli mehaanika ja matemaatika teaduskond geomeetria osakond Kasak V.V. Analüütilise geomeetria töötuba esimestele õpilastele ANALÜÜTILINE GEEOETIA TASANDI ÜLDVÕRRAND. GPD Tasapinna all peame silmas pinda, mille omadus on, et kui sirge kaks punkti kuuluvad tasapinnale, siis kõik sirge punktid kuuluvad antud tasandisse. LOENG 5 ANALÜÜTILISE GEOMEETIA ELEMED. 1 1. Pinna võrrand ja sirge võrrandid ruumis. Võrrandite geomeetriline tähendus Analüütilises geomeetrias käsitletakse mistahes pinda hulgana 1. peatükk LINEAARSED JA TASANDID n R. 1.1. Punktiruumid Varem käsitleti stringide aritmeetilist ruumi.Matemaatikas saab lõplikku järjestatud koordinaatide kogumit tõlgendada mitte ainult Testiülesanne analüütilises geomeetrias. Semester 2. Variant 1 1. Leidke sirge 5x 12y + 1 = 0 paralleelse ringi puutujate võrrandid (x + 3) 2 + (y + 1) 2 = 4. 2. Kirjutage võrrand puutuja Vene Föderatsiooni Haridus- ja Teadusministeerium Föderaalne Riiklik Autonoomne Kõrgharidusasutus "Kaasani (Volga oblast) Föderaalne Ülikool" Kõrge järgu diferentsiaalid. Eksamipilet. Maatriksid, põhimõisted ja definitsioonid .. Kirjutage ringi võrrand, kui punktid A (;) ja B (-; 6) on ühe läbimõõdu otsad .. Antud on tipud ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ Moskva Riiklik Tehnikaülikool nimega N.E. Baumani põhiteaduste teaduskond matemaatilise modelleerimise osakond À.Í. Santnikov, Teise järgu pinnad. Pinda kolmemõõtmelises ruumis kirjeldatakse võrrandiga kujul F (x; y; z) = 0 või z = f (x; y). Kahe pinna ristumiskoht määrab ruumis sirge, s.t. joon ruumis Pärast põhjalikku uurimist sirgjooned tasapinnal jätkame kahemõõtmelise maailma geomeetria uurimist. Panused on kahekordistunud ja kutsun teid külastama maalilist ellipside, hüperboolide, paraboolide galeriid, mis on tüüpilised esindajad. teise järgu read... Ringkäik on juba alanud ja kõigepealt lühiinfo kogu ekspositsiooni kohta muuseumi erinevatel korrustel: Tasapinnal olevat sirget nimetatakse algebraline, kui sisse afiinne koordinaatsüsteem selle võrrandil on vorm, kus on polünoom, mis koosneb vormi liikmetest (- reaalarv, - mittenegatiivsed täisarvud). Nagu näete, ei sisalda algebralise sirge võrrand siinusi, koosinusi, logaritme ega muid funktsionaalseid beau monde. Sisse ainult "x" ja "mängud". mittenegatiivsed täisarvud kraadid. Rea järjekord on võrdne selles sisalduvate terminite maksimaalse väärtusega. Vastava teoreemi kohaselt ei sõltu algebralise sirge mõiste, samuti selle järjekord valikust afiinne koordinaatsüsteem Seetõttu eeldame olemise hõlbustamiseks, et kõik järgnevad arvutused toimuvad aastal Descartes'i koordinaadid. Üldvõrrand teist järku real on vorm, kus Kui, siis võrrand on lihtsustatud Paljud on uute mõistete tähendusest aru saanud, kuid sellegipoolest torkame materjali 100% omastamiseks näpud pistikupessa. Rea järjekorra määramiseks peate kordama kõik tingimused selle võrrandid ja igaühe jaoks leida kraadide summa sissetulevad muutujad. Näiteks: mõiste sisaldab "x" 1. astmes; Nüüd selgitame välja, miks võrrand määrab sirge teiseks tellida: mõiste sisaldab "x" 2. astmes; Maksimaalne väärtus: 2 Kui lisame oma võrrandile lisaks, näiteks, siis see juba määrab kolmanda järjekorra rida... Ilmselt sisaldab kolmandat järku joonevõrrandi üldvorm terminite "täielikku komplekti", mille muutujate astmete summa on võrdne kolmega: Juhul, kui lisame ühe või mitu sobivat terminit, mis sisaldavad 3., 4. ja kõrgema järgu algebraliste ridadega peame tegelema rohkem kui üks kord, eriti kui tutvume polaarkoordinaatide süsteem. Pöördugem siiski tagasi üldvõrrandi juurde ja tuletagem meelde selle lihtsamaid koolivariatsioone. Näidetena pakub end välja parabool, mille võrrandit saab hõlpsasti taandada üldkujuks, ja hüperbool samaväärse võrrandiga. Samas pole kõik nii sujuv... Üldvõrrandi oluline puudus on see, et peaaegu alati on ebaselge, millise sirge see seab. Isegi kõige lihtsamal juhul ei saa te kohe aru, et tegemist on hüperbooliga. Sellised paigutused on head ainult maskeraadi korral, seetõttu käsitletakse analüütilise geomeetria käigus tüüpilist probleemi teist järku rea võrrandi taandamine kanoonilisele kujule. See on võrrandi üldtunnustatud standardvorm, kui mõne sekundiga saab selgeks, millise geomeetrilise objekti see määratleb. Lisaks on kanooniline vaade väga mugav paljude praktiliste ülesannete lahendamiseks. Nii näiteks kanoonilise võrrandi järgi "Lame" sirge, esiteks on kohe selge, et tegemist on sirgjoonega ja teiseks on selle juurde kuuluv punkt ja suunavektor hästi näha. Ilmselgelt mis tahes 1. järjekorra rida on sirgjoon. Teisel korrusel ei oota meid aga mitte tunnimees, vaid hoopis mitmekesisem üheksast kujust koosnev seltskond: Spetsiaalse toimingute komplekti abil taandatakse mis tahes teist järku rea võrrand ühele järgmistest tüüpidest: (ja on positiivsed reaalarvud) 1) 2) - kanooniline hüperbooli võrrand; 3) 4) – kujuteldav ellips; 5) - ristuvate sirgjoonte paar; 6) - paar kujuteldav ristuvad sirged (ainsa kehtiva lõikepunktiga alguspunktis); 7) - paralleelsete sirgjoonte paar; 8) - paar kujuteldav paralleelsed jooned; 9) - kokkulangevate sirgjoonte paar. Mõnele lugejale võib jääda mulje, et nimekiri on puudulik. Näiteks punktis 7 võrrand määrab paari otsene teljega paralleelne ja tekib küsimus: kus on võrrand, mis määrab ordinaadiga paralleelsed sirged? Vasta sellele ei peeta kanooniliseks... Sirged jooned tähistavad sama standardset korpust, pööratuna 90 kraadi, ja klassifikatsiooni lisakanne on üleliigne, kuna see ei sisalda midagi põhimõtteliselt uut. Seega on teist tüüpi ridu üheksa ja ainult üheksa, kuid praktikas on kõige levinumad ellips, hüperbool ja parabool. Vaatame kõigepealt ellipsi. Nagu tavaliselt, keskendun punktidele, millel on ülesannete lahendamisel suur tähtsus, ja kui vajate üksikasjalikku valemite tuletamist, teoreemide tõestust, vaadake näiteks Bazylevi / Atanasjani või Aleksandrovi õpikut. Õigekiri ... palun ärge korrake mõnede Yandexi kasutajate vigu, kes on huvitatud "ellipsi ehitamisest", "ellipsi ja ovaali erinevusest" ning "elebsi ekstsentrilisusest". Ellipsi kanoonilisel võrrandil on vorm, kus on positiivsed reaalarvud ja. Ma sõnastan ellipsi definitsiooni hiljem, kuid praegu on aeg rääkida poest paus ja lahendada levinud probleem: Jah, võtke see ja lihtsalt joonistage see. Ülesandega puututakse sageli kokku ja märkimisväärne osa õpilastest ei tule joonistusega päris asjatundlikult toime: Näide 1 Koostage võrrandiga antud ellips Lahendus: kõigepealt toome võrrandi kanoonilisele kujule: Miks viia? Üks kanoonilise võrrandi eeliseid on see, et see võimaldab teil koheselt määrata ellipsi tipud mis on punktides. On lihtne näha, et kõigi nende punktide koordinaadid vastavad võrrandile. Sel juhul : Et kiiresti ette kujutada, kuidas see või teine ellips välja näeb, piisab, kui vaadata selle kanoonilise võrrandi väärtusi "a" ja "bs". Kõik on korras, kokkupandav ja ilus, kuid on üks hoiatus: tegin joonise programmi abil. Ja saate joonist täiendada mis tahes rakendusega. Karmis reaalsuses on aga laual ruuduline paber ja meie kätel tantsivad ringides hiired. Kunstiandidega inimesed võivad muidugi vaielda, aga teil on ka hiiri (kuigi väiksemaid). Pole asjata, et inimkond on leiutanud joonlaua, kompassid, kraadiklaasi ja muud lihtsad joonistusseadmed. Sel põhjusel ei suuda me tõenäoliselt ellipsi täpselt joonistada, teades ainult tippe. Ikka hästi, kui ellips on väike, näiteks pooltelgedega. Teise võimalusena saate vähendada joonise mõõtkava ja vastavalt sellele ka mõõtmeid. Kuid üldiselt on väga soovitav leida lisapunkte. Ellipsi konstrueerimiseks on kaks lähenemisviisi – geomeetriline ja algebraline. Mulle ei meeldi kompassi ja joonlaua abil ehitamine mitte kõige lühema algoritmi ja joonise olulise segaduse tõttu. Hädaolukorras palume tutvuda õpikuga, kuid tegelikult on palju ratsionaalsem kasutada algebra vahendeid. Avaldage mustandil olevast ellipsi võrrandist kiiresti: Lisaks jaguneb võrrand kaheks funktsiooniks: Kanoonilise võrrandiga määratud ellips on sümmeetriline nii koordinaatide telgede kui ka alguspunkti suhtes. Ja see on suurepärane – sümmeetria on peaaegu alati tasuta kingituste esilekutsuja. Ilmselgelt piisab 1. koordinaatide kvartaliga tegelemisest, seega on funktsiooni vaja Märkige joonisele punktid (punane), ülejäänud kaaredele sümmeetrilised punktid (sinine) ja ühendage kogu ettevõte hoolikalt joonega: Ellips on ovaali erijuhtum. Sõna "ovaal" ei tohiks mõista vilisti tähenduses ("laps joonistas ovaali" jne). See on matemaatiline termin, millel on üksikasjalik sõnastus. Selle tunni eesmärk ei ole käsitleda ovaalide teooriat ja nende erinevaid tüüpe, mis on analüütilise geomeetria tavakursusel peaaegu tähelepanuta jäetud. Ja vastavalt asjakohasematele vajadustele liigume otse ellipsi range määratluse juurde: Ellips Kas tasandi kõigi punktide hulk, mille kauguste summa iga punktini on kahest etteantud punktist, nn. trikid ellips, - on konstantne väärtus, mis on arvuliselt võrdne selle ellipsi peatelje pikkusega:. Nüüd saab kõik selgemaks: Kujutage ette, et sinine täpp "juhib" ellipsi. Seega, olenemata sellest, millise ellipsi punkti me võtame, on segmentide pikkuste summa alati sama: Teeme kindlaks, et meie näites on summa väärtus tõesti võrdne kaheksaga. Asetage mõtteliselt punkt "em" ellipsi paremasse tippu, seejärel:, mida soovite kontrollida. Teine viis selle joonistamiseks põhineb ellipsi määratlusel. Kõrgem matemaatika põhjustab mõnikord pingeid ja stressi, seega on aeg korraldada uus mahalaadimise seanss. Palun võtke Whatmani paber või suur tükk pappi ja kinnitage see kahe naastudega laua külge. Need saavad olema trikid. Siduge väljaulatuvate naelapeade külge roheline niit ja tõmmake see pliiatsiga lõpuni. Pliiatsi kael on mingil hetkel, mis kuulub ellipsi alla. Nüüd hakake oma pliiatsit paberilehele tõmbama, hoides rohelist niiti pingul. Jätkake protsessi, kuni jõuate tagasi alguspunkti ... suurepärane ... joonise saab esitada õpetajale kontrollimiseks =) Antud näites olen kujutanud "valmis" fookuspunkte ja nüüd õpime, kuidas neid geomeetria sügavustest eraldada. Kui ellips on antud kanoonilise võrrandiga, siis on selle fookustel koordinaadid Arvutamine on lihtsam kui aurutatud naeris: ! Fookuste konkreetseid koordinaate ei saa identifitseerida tähendusega "tse"! Kordan, et see on nii KAUGUS igast fookusest keskpunktini(mis üldjuhul ei pea asuma täpselt lähtekohas). Ellipsi ekstsentrilisus on suhe, mis võib võtta väärtusi sees. Meie puhul: Uurime välja, kuidas ellipsi kuju sõltub selle ekstsentrilisusest. Selle jaoks fikseerige vasak ja parem tipp vaadeldav ellips, see tähendab, et poolsuurtelje väärtus jääb konstantseks. Siis on ekstsentrilisuse valem järgmine:. Alustame ekstsentrilisuse väärtuse ühtsusele lähemale toomist. See on võimalik ainult siis, kui. Mida see tähendab? ... pidage meeles võlutrikke Seega mida lähemal on ellipsi ekstsentrilisuse väärtus ühtsusele, seda piklikum on ellips. Nüüd simuleerime vastupidist protsessi: ellipsi fookused. Seega mida lähemal on ekstsentrilisuse väärtus nullile, seda rohkem näeb ellips välja... vaadake äärmuslikku juhtumit, kus fookused on päritolus edukalt taasühendatud: Tõepoolest, pooltelgede võrdsuse korral saab ellipsi kanooniline võrrand kuju, mis teisendatakse refleksiivselt koolist hästi tuntud võrrandiks ringist, mille keskpunkt asub raadiuse "a" koordinaatide lähtepunktis. Praktikas kasutatakse sagedamini salvestust "rääkiva" tähega "er":. Raadius on lõigu pikkus, kusjuures iga ringi punkt on raadiuse kauguse võrra keskelt eemaldatud. Pange tähele, et ellipsi määratlus jääb täiesti õigeks: fookused langevad kokku ja iga ringi punkti kokkulangevate segmentide pikkuste summa on konstantne väärtus. Kuna fookuste vaheline kaugus, siis mis tahes ringi ekstsentrilisus on null. Ring ehitatakse lihtsalt ja kiiresti, piisab, kui relvastada end kompassiga. Sellegipoolest on mõnikord vaja välja selgitada mõne selle punkti koordinaadid, sel juhul läheme tuttavat teed - toome võrrandi kiirele Matani vormile: Seejärel leiame vajalikud väärtused, eristama, integreerida ja teha muid häid asju. Artikkel on muidugi ainult viitamiseks, aga kuidas saab elada ilma armastuseta? Loominguline ülesanne iseseisvaks lahenduseks Näide 2 Kirjutage ellipsi kanooniline võrrand, kui üks selle fookustest ja pool-minoortelg on teada (keskpunkt on lähtepunktis). Otsige üles tipud, lisapunktid ja tõmmake joonisele joon. Arvutage ekstsentrilisus. Lahendus ja joonistamine tunni lõpus Lisame toimingu: Tuleme tagasi ellipsi kanoonilise võrrandi juurde, nimelt tingimuse juurde, mille mõistatus on piinanud uudishimulikke mõistusi selle kõvera esmamainimisest saadik. Siin uurisime ellipsit Selline võrrand on haruldane, kuid see tuleb ette. Ja see tõesti määratleb ellipsi. Hajutame müstika:
A 1 (, 0)
A2 (-, 0)
Seetõttu asuvad kõik ellipsi punktid ristküliku sees, mille moodustavad sirged x = ±, y = ± b. (Joonis 2.)
B 2 (0, b)
 ei ole samal ajal võrdsed nulliga. Seda rida nimetatakse kõver või teise järgu rida.
ei ole samal ajal võrdsed nulliga. Seda rida nimetatakse kõver või teise järgu rida.
 reaalkoordinaatidega, mis vastavad võrrandile (1). Sel juhul loetakse võrrand (1) määratlemaks teist järku kujuteldavat joont. Näiteks,
reaalkoordinaatidega, mis vastavad võrrandile (1). Sel juhul loetakse võrrand (1) määratlemaks teist järku kujuteldavat joont. Näiteks, 
see on kujuteldava ringi võrrand.
see on kujuteldava ringi võrrand.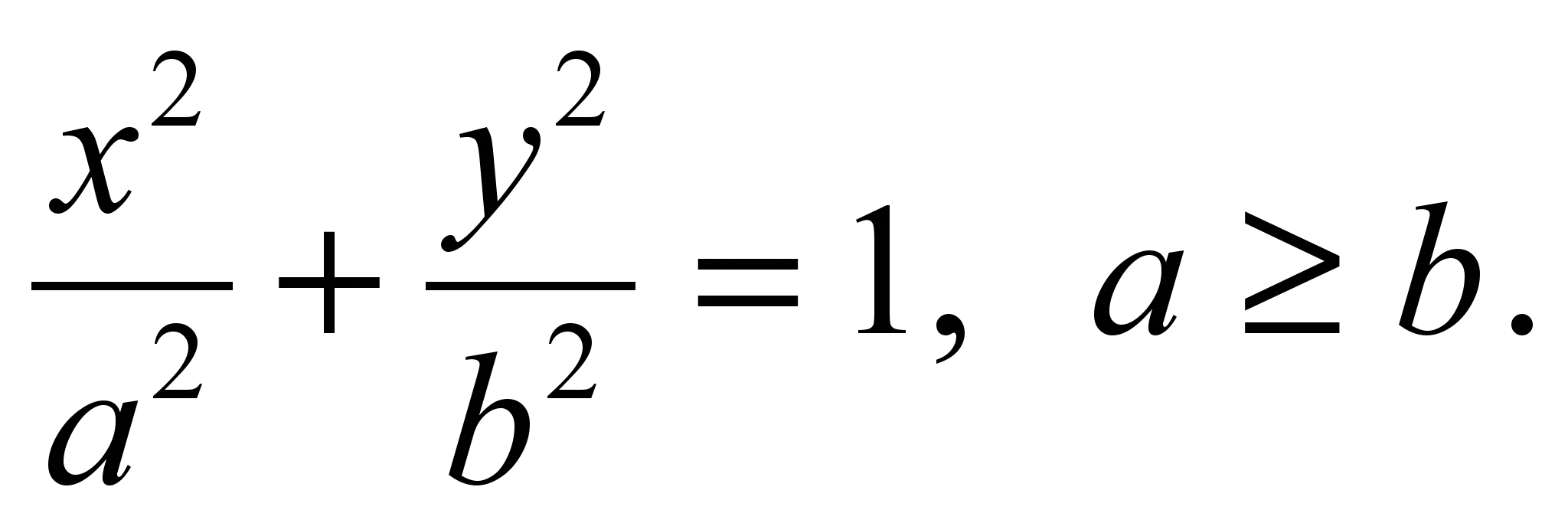 (2)
(2)
 ja märkige teljel O NSpunktid
ja märkige teljel O NSpunktid 
 helistas trikid ellips. Siis saab ellipsi määratleda kui
helistas trikid ellips. Siis saab ellipsi määratleda kui juures
juures

ellipsi praegune punkt. Sel juhul saame Siis võrdsus peab olema täidetud
ellipsi praegune punkt. Sel juhul saame Siis võrdsus peab olema täidetud
 , siis
, siis (4)
(4)
 , saame lõpuks ellipsi kanoonilise võrrandi
, saame lõpuks ellipsi kanoonilise võrrandi 
 Ilmselgelt läbib ellips punkte
Ilmselgelt läbib ellips punkte  ... Olles esimeses kvartalis skemaatilise ehituse lõpetanud, kuvame selle graafiku sümmeetriliselt kõigis kvartalites. Seega on ellips pidev suletud kõver. Punkte nimetatakse ellipsi tipud.
... Olles esimeses kvartalis skemaatilise ehituse lõpetanud, kuvame selle graafiku sümmeetriliselt kõigis kvartalites. Seega on ellips pidev suletud kõver. Punkte nimetatakse ellipsi tipud. helistasekstsentrilisusellips. Ellipsi jaoks
helistasekstsentrilisusellips. Ellipsi jaoks  .
.
 kutsutakse ellipsi suund.
kutsutakse ellipsi suund.
 on ellipsi erijuht. Temale
on ellipsi erijuht. Temale 

 , märkige teljel O NSpunktid
, märkige teljel O NSpunktid  helistas trikid hüperbool. Siis saab hüperbooli defineerida kui
helistas trikid hüperbool. Siis saab hüperbooli defineerida kui
 juures
juures

 Sellest võrrandist on näha, et piisavalt suurNShüperbool on sirgele lähedane
Sellest võrrandist on näha, et piisavalt suurNShüperbool on sirgele lähedane  ... Pärast skemaatilist ehitamist esimeses kvartalis kuvame graafiku sümmeetriliselt kõigis kvartalites.
... Pärast skemaatilist ehitamist esimeses kvartalis kuvame graafiku sümmeetriliselt kõigis kvartalites. kutsutakse tipud hüperbool. Otsene
kutsutakse tipud hüperbool. Otsene  kutsutakse asümptoodid - need on sirged jooned, millele hüperbooli oksad kalduvad, ilma neid ületamata.
kutsutakse asümptoodid - need on sirged jooned, millele hüperbooli oksad kalduvad, ilma neid ületamata. .
.
 .
.
 a
a
 need. võrrandisse (1) tuleb panna
need. võrrandisse (1) tuleb panna koefitsientR helistas TOjuures
koefitsientR helistas TOjuures
 nimetatakse fookuseks
nimetatakse fookuseks ellips;
ellips; parabool;
parabool;
Ärakiri
Teise järgu read.
Ellips ja selle kanooniline võrrand. RingAlgebralise sirge mõiste ja selle järjekord
![]() - suvalised reaalarvud (on tavaks kirjutada kordajaga - "kaks"), ja koefitsiendid ei ole samal ajal võrdsed nulliga.
- suvalised reaalarvud (on tavaks kirjutada kordajaga - "kaks"), ja koefitsiendid ei ole samal ajal võrdsed nulliga.![]() , ja kui koefitsiendid ei ole samaaegselt võrdsed nulliga, siis see on täpselt nii "lame" sirge üldvõrrand mis on esimese järjekorra rida.
, ja kui koefitsiendid ei ole samaaegselt võrdsed nulliga, siis see on täpselt nii "lame" sirge üldvõrrand mis on esimese järjekorra rida.
mõiste sisaldab 1. astmes "ulukit";
terminis pole muutujaid, seega on nende astmete summa null.
liidetavas on muutujate astmete summa: 1 + 1 = 2;
mõiste sisaldab 2. astmes "ulukit";
kõik muud tingimused - vähem kraadi.
, kus koefitsiendid ei ole samal ajal võrdsed nulliga.![]() , siis räägime sellest 4. järjekorra read, jne.
, siis räägime sellest 4. järjekorra read, jne.Mis on võrrandi kanooniline vorm?
Teist järku ridade klassifikatsioon
![]() - ellipsi kanooniline võrrand;
- ellipsi kanooniline võrrand;![]() - parabooli kanooniline võrrand;
- parabooli kanooniline võrrand;Ellips ja selle kanooniline võrrand
Kuidas ehitada ellipsi?
![]()

jaotis kutsutakse suurtelg ellips;
osa – väiketelg;
number ![]() kutsutakse poolsuurtelg ellips;
kutsutakse poolsuurtelg ellips;
number ![]() – pool-minoortelg.
– pool-minoortelg.
meie näites:.
![]() - määrab ellipsi ülemise kaare;
- määrab ellipsi ülemise kaare; ![]() - määrab ellipsi alumise kaare.
- määrab ellipsi alumise kaare.![]() ... Abstsissidega lisapunktide leidmine viitab iseenesest
... Abstsissidega lisapunktide leidmine viitab iseenesest ![]() ... Saime kalkulaatorisse kolm sms-i:
... Saime kalkulaatorisse kolm sms-i: 
Meeldiv on muidugi ka see, et kui arvutustes tehakse ränk viga, selgub see kohe ehituse käigus.
Parem on joonistada esialgne visand õhukeselt ja õhukeselt ning alles seejärel vajutada pliiatsit. Tulemuseks peaks olema korralik ellips. Muide, kas soovite teada, mis see kõver on?Ellipsi definitsioon. Ellipsi fookused ja ellipsi ekstsentrilisus
Sel juhul on fookuste vaheline kaugus väiksem kui see väärtus:.
Kuidas leida ellipsi fookusi?
![]() , kus see on kaugus igast fookusest ellipsi sümmeetria keskpunktini.
, kus see on kaugus igast fookusest ellipsi sümmeetria keskpunktini.![]()
Ja seetõttu ei saa fookuste vahelist kaugust siduda ka ellipsi kanoonilise asendiga. Teisisõnu, ellipsi saab teisaldada teise kohta ja väärtus jääb muutumatuks, samas kui fookused muudavad loomulikult oma koordinaate. Pidage seda teemat edasi uurides meeles.Ellipsi ekstsentrilisus ja selle geomeetriline tähendus
![]() ... See tähendab, et ellipsi fookused "liiguvad lahku" mööda abstsisstelge külgmiste tippudeni. Ja kuna "rohelised segmendid ei ole kummist", hakkab ellips paratamatult tasanema, muutudes teljele nööritud ja õhemaks vorstiks.
... See tähendab, et ellipsi fookused "liiguvad lahku" mööda abstsisstelge külgmiste tippudeni. Ja kuna "rohelised segmendid ei ole kummist", hakkab ellips paratamatult tasanema, muutudes teljele nööritud ja õhemaks vorstiks.![]() läksid üksteise poole, lähenedes keskusele. See tähendab, et "tse" väärtus muutub üha väiksemaks ja vastavalt sellele kipub ekstsentrilisus nulli:.
läksid üksteise poole, lähenedes keskusele. See tähendab, et "tse" väärtus muutub üha väiksemaks ja vastavalt sellele kipub ekstsentrilisus nulli:.
Sel juhul "rohelised segmendid" "muutuvad rahvarohkeks" ja hakkavad ellipsi joont üles ja alla "tõukama".
Ring on ellipsi erijuht
- ülemise poolringi funktsioon;
- alumise poolringi funktsioon.Ellipsi pöörlemine ja paralleeltõlge
![]() , kuid see pole praktikas see võrrand
, kuid see pole praktikas see võrrand ![]() ? Ju tundub, et ka siin on nagu ellips!
? Ju tundub, et ka siin on nagu ellips!
Ehituse tulemusena saadakse meie loomulik ellips, mis on pööratud 90 kraadi võrra. See on, ![]() - see on mittekanooniline märge ellips
- see on mittekanooniline märge ellips ![]() . Rekord!- võrrand
. Rekord!- võrrand ![]() ei defineeri ühtegi teist ellipsi, kuna teljel pole punkte (fookusi), mis rahuldaksid ellipsi definitsiooni.
ei defineeri ühtegi teist ellipsi, kuna teljel pole punkte (fookusi), mis rahuldaksid ellipsi definitsiooni.