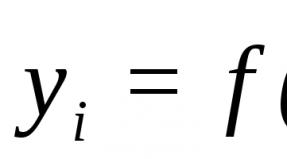Inverse matrix algorithm for calculating the inverse matrix. Inverse matrix. Solution of matrix equations. Using the attached matrix

20.06.2022 Preparations

The matrix $A^(-1)$ is called the inverse of the square matrix $A$ if $A^(-1)\cdot A=A\cdot A^(-1)=E$, where $E $ is the identity matrix, the order of which is equal to the order of the matrix $A$.

A non-singular matrix is a matrix whose determinant is not equal to zero. Accordingly, a degenerate matrix is one whose determinant is equal to zero.

The inverse matrix $A^(-1)$ exists if and only if the matrix $A$ is nonsingular. If the inverse matrix $A^(-1)$ exists, then it is unique.

There are several ways to find the inverse of a matrix, and we'll look at two of them. On this page, we will consider the adjoint matrix method, which is considered standard in most higher mathematics courses. The second way to find the inverse matrix (method of elementary transformations), which involves the use of the Gauss method or the Gauss-Jordan method, is considered in the second part.

Adjoint (union) matrix method

Let the matrix $A_(n\times n)$ be given. In order to find the inverse matrix $A^(-1)$, three steps are required:

Find the determinant of the matrix $A$ and make sure that $\Delta A\neq 0$, i.e. that the matrix A is nondegenerate.
Compose algebraic complements $A_(ij)$ of each element of the matrix $A$ and write down the matrix $A_(n\times n)^(*)=\left(A_(ij) \right)$ from the found algebraic complements.
Write the inverse matrix taking into account the formula $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$.

The matrix $(A^(*))^T$ is often referred to as the adjoint (mutual, allied) matrix of $A$.

If the decision is made manually, then the first method is good only for matrices of relatively small orders: second (), third (), fourth (). To find the inverse matrix for a higher order matrix, other methods are used. For example, the Gauss method, which is discussed in the second part.

Example #1

Find matrix inverse to matrix $A=\left(\begin(array) (cccc) 5 & -4 &1 & 0 \\ 12 &-11 &4 & 0 \\ -5 & 58 &4 & 0 \\ 3 & - 1 & -9 & 0 \end(array) \right)$.

Since all elements of the fourth column are equal to zero, then $\Delta A=0$ (i.e. the matrix $A$ is degenerate). Since $\Delta A=0$, there is no matrix inverse to $A$.

Answer: matrix $A^(-1)$ does not exist.

Example #2

Find the matrix inverse to the matrix $A=\left(\begin(array) (cc) -5 & 7 \\ 9 & 8 \end(array)\right)$. Run a check.

We use the adjoint matrix method. First, let's find the determinant of the given matrix $A$:

$$ \Delta A=\left| \begin(array) (cc) -5 & 7\\ 9 & 8 \end(array)\right|=-5\cdot 8-7\cdot 9=-103. $$

Since $\Delta A \neq 0$, then the inverse matrix exists, so we continue the solution. Finding Algebraic Complements

\begin(aligned) & A_(11)=(-1)^2\cdot 8=8; \; A_(12)=(-1)^3\cdot 9=-9;\\ & A_(21)=(-1)^3\cdot 7=-7; \; A_(22)=(-1)^4\cdot (-5)=-5.\\ \end(aligned)

Compose a matrix of algebraic complements: $A^(*)=\left(\begin(array) (cc) 8 & -9\\ -7 & -5 \end(array)\right)$.

Transpose the resulting matrix: $(A^(*))^T=\left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right)$ (the resulting matrix is often is called the adjoint or union matrix to the matrix $A$). Using the formula $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$, we have:

$$ A^(-1)=\frac(1)(-103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right) =\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right) $$

So the inverse matrix is found: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right) $. To check the truth of the result, it is enough to check the truth of one of the equalities: $A^(-1)\cdot A=E$ or $A\cdot A^(-1)=E$. Let's check the equality $A^(-1)\cdot A=E$. In order to work less with fractions, we will substitute the matrix $A^(-1)$ not in the form $\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \ end(array)\right)$ but as $-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array )\right)$:

$$ A^(-1)\cdot(A) =-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end( array)\right)\cdot\left(\begin(array) (cc) -5 & 7 \\ 9 & 8 \end(array)\right) =-\frac(1)(103)\cdot\left( \begin(array) (cc) -103 & 0 \\ 0 & -103 \end(array)\right) =\left(\begin(array) (cc) 1 & 0 \\ 0 & 1 \end(array )\right) =E $$

Answer: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right)$.

Example #3

Find the inverse of the matrix $A=\left(\begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \right)$. Run a check.

Let's start by calculating the determinant of the matrix $A$. So, the determinant of the matrix $A$ is:

$$ \Delta A=\left| \begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \right| = 18-36+56-12=26. $$

Since $\Delta A\neq 0$, then the inverse matrix exists, so we continue the solution. We find the algebraic complements of each element of the given matrix:

We compose a matrix of algebraic additions and transpose it:

$$ A^*=\left(\begin(array) (ccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37\end(array) \right); \; (A^*)^T=\left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right) . $$

Using the formula $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$, we get:

$$ A^(-1)=\frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37\end(array) \right)= \left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \end(array) \right) $$

So $A^(-1)=\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6/13 & -3/26 & 37/26 \end(array) \right)$. To check the truth of the result, it is enough to check the truth of one of the equalities: $A^(-1)\cdot A=E$ or $A\cdot A^(-1)=E$. Let's check the equality $A\cdot A^(-1)=E$. In order to work less with fractions, we will substitute the matrix $A^(-1)$ not in the form $\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \end(array) \right)$, but as $\frac(1)(26)\cdot \left( \begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right)$:

$$ A\cdot(A^(-1)) =\left(\begin(array)(ccc) 1 & 7 & 3 \\ -4 & 9 & 4\\ 0 & 3 & 2\end(array) \right)\cdot \frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\ end(array) \right) =\frac(1)(26)\cdot\left(\begin(array) (ccc) 26 & 0 & 0 \\ 0 & 26 & 0 \\ 0 & 0 & 26\end (array) \right) =\left(\begin(array) (ccc) 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end(array) \right) =E $$

The check was passed successfully, the inverse matrix $A^(-1)$ was found correctly.

Answer: $A^(-1)=\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6 /13 & -3/26 & 37/26 \end(array) \right)$.

Example #4

Find matrix inverse of $A=\left(\begin(array) (cccc) 6 & -5 & 8 & 4\\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7\\ -4 & 8 & -8 & -3 \end(array) \right)$.

For a matrix of the fourth order, finding the inverse matrix using algebraic additions is somewhat difficult. However, such examples are found in the control works.

To find the inverse matrix, first you need to calculate the determinant of the matrix $A$. The best way to do this in this situation is to expand the determinant in a row (column). We select any row or column and find the algebraic complement of each element of the selected row or column.

For example, for the first row we get:

$$ A_(11)=\left|\begin(array)(ccc) 7 & 5 & 2\\ 5 & 3 & 7\\ 8 & -8 & -3 \end(array)\right|=556; \; A_(12)=-\left|\begin(array)(ccc) 9 & 5 & 2\\ 7 & 3 & 7 \\ -4 & -8 & -3 \end(array)\right|=-300 ; $$ $$ A_(13)=\left|\begin(array)(ccc) 9 & 7 & 2\\ 7 & 5 & 7\\ -4 & 8 & -3 \end(array)\right|= -536;\; A_(14)=-\left|\begin(array)(ccc) 9 & 7 & 5\\ 7 & 5 & 3\\ -4 & 8 & -8 \end(array)\right|=-112. $$

The determinant of the matrix $A$ is calculated by the following formula:

$$ \Delta(A)=a_(11)\cdot A_(11)+a_(12)\cdot A_(12)+a_(13)\cdot A_(13)+a_(14)\cdot A_(14 )=6\cdot 556+(-5)\cdot(-300)+8\cdot(-536)+4\cdot(-112)=100. $$

$$ \begin(aligned) & A_(21)=-77;\;A_(22)=50;\;A_(23)=87;\;A_(24)=4;\\ & A_(31) =-93;\;A_(32)=50;\;A_(33)=83;\;A_(34)=36;\\ & A_(41)=473;\;A_(42)=-250 ;\;A_(43)=-463;\;A_(44)=-96. \end(aligned) $$

Algebraic complement matrix: $A^*=\left(\begin(array)(cccc) 556 & -300 & -536 & -112\\ -77 & 50 & 87 & 4 \\ -93 & 50 & 83 & 36\\ 473 & -250 & -463 & -96\end(array)\right)$.

Attached matrix: $(A^*)^T=\left(\begin(array) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96\end(array)\right)$.

Inverse matrix:

$$ A^(-1)=\frac(1)(100)\cdot \left(\begin(array) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96 \end(array) \right)= \left(\begin(array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/ 25 & 1/25 & 9/25 & -24/25 \end(array) \right) $$

Checking, if desired, can be done in the same way as in the previous examples.

Answer: $A^(-1)=\left(\begin(array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/25 & 1/25 & 9/25 & -24/25 \end(array) \right) $.

In the second part, another way of finding the inverse matrix will be considered, which involves the use of transformations of the Gauss method or the Gauss-Jordan method.

Matrix A -1 is called the inverse matrix with respect to matrix A, if A * A -1 \u003d E, where E is the identity matrix of the nth order. The inverse matrix can only exist for square matrices.

Service assignment. Using this service online, you can find algebraic additions, transposed matrix A T , union matrix and inverse matrix. The solution is carried out directly on the site (online) and is free. The calculation results are presented in a report in Word format and in Excel format (that is, it is possible to check the solution). see design example.

Instruction. To obtain a solution, you must specify the dimension of the matrix. Next, in the new dialog box, fill in the matrix A .

See also Inverse Matrix by the Jordan-Gauss Method

Algorithm for finding the inverse matrix

Finding the transposed matrix A T .
Definition of algebraic additions. Replace each element of the matrix with its algebraic complement.
Composing an inverse matrix from algebraic additions: each element of the resulting matrix is divided by the determinant of the original matrix. The resulting matrix is the inverse of the original matrix.

Next inverse matrix algorithm similar to the previous one, except for some steps: first, the algebraic complements are calculated, and then the union matrix C is determined.

Determine if the matrix is square. If not, then there is no inverse matrix for it.
Calculation of the determinant of the matrix A . If it is not equal to zero, we continue the solution, otherwise, the inverse matrix does not exist.
Definition of algebraic additions.
Filling in the union (mutual, adjoint) matrix C .
Compilation of the inverse matrix from algebraic additions: each element of the adjoint matrix C is divided by the determinant of the original matrix. The resulting matrix is the inverse of the original matrix.
Make a check: multiply the original and the resulting matrices. The result should be an identity matrix.

Example #1. We write the matrix in the form:

Algebraic additions. ∆ 1,2 = -(2 4-(-2 (-2))) = -4 ∆ 2,1 = -(2 4-5 3) = 7 ∆ 2,3 = -(-1 5-(-2 2)) = 1 ∆ 3,2 = -(-1 (-2)-2 3) = 4

A -1 =

0,6	-0,4	0,8
0,7	0,2	0,1
-0,1	0,4	-0,3

Another algorithm for finding the inverse matrix

We present another scheme for finding the inverse matrix.

Find the determinant of the given square matrix A .
We find algebraic additions to all elements of the matrix A .
We write the algebraic complements of the elements of the rows into the columns (transposition).
We divide each element of the resulting matrix by the determinant of the matrix A .

As you can see, the transposition operation can be applied both at the beginning, over the original matrix, and at the end, over the resulting algebraic additions.

A special case: The inverse, with respect to the identity matrix E , is the identity matrix E .

We continue talking about actions with matrices. Namely, in the course of studying this lecture, you will learn how to find the inverse matrix. Learn. Even if the math is tight.

What is an inverse matrix? Here we can draw an analogy with reciprocals: consider, for example, the optimistic number 5 and its reciprocal. The product of these numbers is equal to one: . It's the same with matrices! The product of a matrix and its inverse is - identity matrix, which is the matrix analogue of the numerical unit. However, first things first, we will solve an important practical issue, namely, we will learn how to find this very inverse matrix.

What do you need to know and be able to find the inverse matrix? You must be able to decide determinants. You must understand what is matrix and be able to perform some actions with them.

There are two main methods for finding the inverse matrix:
by using algebraic additions and using elementary transformations.

Today we will study the first, easier way.

Let's start with the most terrible and incomprehensible. Consider square matrix . The inverse matrix can be found using the following formula:

Where is the determinant of the matrix , is the transposed matrix of algebraic complements of the corresponding elements of the matrix .

The concept of an inverse matrix exists only for square matrices, matrices "two by two", "three by three", etc.

Notation: As you probably already noticed, the inverse of a matrix is denoted by a superscript

Let's start with the simplest case - a two-by-two matrix. Most often, of course, "three by three" is required, but, nevertheless, I strongly recommend studying a simpler task in order to learn the general principle of the solution.

Example:

Find the inverse of a matrix

We decide. The sequence of actions is conveniently decomposed into points.

1) First we find the determinant of the matrix.

If the understanding of this action is not good, read the material How to calculate the determinant?

Important! If the determinant of the matrix is ZERO– inverse matrix DOES NOT EXIST.

In the example under consideration, as it turned out, , which means that everything is in order.

2) Find the matrix of minors.

To solve our problem, it is not necessary to know what a minor is, however, it is advisable to read the article How to calculate the determinant.

The matrix of minors has the same dimensions as the matrix , that is, in this case .
The case is small, it remains to find four numbers and put them instead of asterisks.

Back to our matrix
Let's look at the top left element first:

How to find it minor?
And this is done like this: MENTALLY cross out the row and column in which this element is located:

The remaining number is minor of the given element, which we write in our matrix of minors:

Consider the following matrix element:

Mentally cross out the row and column in which this element is located:

What remains is the minor of this element, which we write into our matrix:

Similarly, we consider the elements of the second row and find their minors:

Ready.

It's simple. In the matrix of minors, you need CHANGE SIGNS for two numbers:

It is these numbers that I have circled!

is the matrix of algebraic complements of the corresponding elements of the matrix .

And just something…

4) Find the transposed matrix of algebraic additions.

is the transposed matrix of algebraic complements of the corresponding elements of the matrix .

5) Answer.

Remember our formula
All found!

So the inverse matrix is:

It's best to leave the answer as is. NO NEED divide each element of the matrix by 2, as fractional numbers will be obtained. This nuance is discussed in more detail in the same article. Actions with matrices.

How to check the solution?

Matrix multiplication must be performed either

Examination:

already mentioned identity matrix is a matrix with units on main diagonal and zeros elsewhere.

Thus, the inverse matrix is found correctly.

If you perform an action, then the result will also be an identity matrix. This is one of the few cases where matrix multiplication is permutable, more information can be found in the article Properties of operations on matrices. Matrix expressions. Also note that during the check, the constant (fraction) is brought forward and processed at the very end - after the matrix multiplication. This is a standard take.

Let's move on to a more common case in practice - the three-by-three matrix:

Example:

Find the inverse of a matrix

The algorithm is exactly the same as for the two-by-two case.

We find the inverse matrix by the formula: , where is the transposed matrix of algebraic complements of the corresponding elements of the matrix .

1) Find the matrix determinant.

Here the determinant is revealed on the first line.

Also, do not forget that, which means that everything is fine - inverse matrix exists.

2) Find the matrix of minors.

The matrix of minors has the dimension "three by three" , and we need to find nine numbers.

I'll take a look at a couple of minors in detail:

Consider the following matrix element:

MENTALLY cross out the row and column in which this element is located:

The remaining four numbers are written in the determinant "two by two"

This two-by-two determinant and is a minor of the given element. It needs to be calculated:

Everything, the minor is found, we write it into our matrix of minors:

As you may have guessed, there are nine two-by-two determinants to calculate. The process, of course, is dreary, but the case is not the most difficult, it can be worse.

Well, to consolidate - finding another minor in the pictures:

Try to calculate the rest of the minors yourself.

Final Result:
is the matrix of minors of the corresponding elements of the matrix .

The fact that all the minors turned out to be negative is pure coincidence.

3) Find the matrix of algebraic additions.

In the matrix of minors, it is necessary CHANGE SIGNS strictly for the following elements:

In this case:

Finding the inverse matrix for the “four by four” matrix is not considered, since only a sadistic teacher can give such a task (for the student to calculate one “four by four” determinant and 16 “three by three” determinants). In my practice, there was only one such case, and the customer of the test paid for my torment quite dearly =).

In a number of textbooks, manuals, you can find a slightly different approach to finding the inverse matrix, but I recommend using the above solution algorithm. Why? Because the probability of getting confused in calculations and signs is much less.

For inverse matrix there is an apt analogy with the reciprocal of a number. For every number a, which is not equal to zero, there exists a number b that the work a and b equal to one: ab= 1 . Number b is called the reciprocal of a number b. For example, for the number 7, the inverse is the number 1/7, since 7*1/7=1.

inverse matrix , which is required to be found for a given square matrix BUT, such a matrix is called

the product by which the matrices BUT on the right is the identity matrix, i.e.,
. (1)

An identity matrix is a diagonal matrix in which all diagonal entries are equal to one.

Finding the inverse matrix- a problem that is most often solved by two methods:

the method of algebraic additions, in which it is required to find determinants and transpose matrices;
Gaussian elimination of unknowns, which requires elementary transformations of matrices (add rows, multiply rows by the same number, etc.).

For those who are especially curious, there are other methods, for example, the method of linear transformations. In this lesson, we will analyze the three methods mentioned and algorithms for finding the inverse matrix by these methods.

Theorem.For each non-singular (non-singular, non-singular) square matrix, one can find an inverse matrix, and moreover, only one. For a special (degenerate, singular) square matrix, the inverse matrix does not exist.

The square matrix is called non-special(or non-degenerate, non-singular) if its determinant is not equal to zero, and special(or degenerate, singular) if its determinant is zero.

The inverse matrix can only be found for a square matrix. Naturally, the inverse matrix will also be square and of the same order as the given matrix. A matrix for which an inverse matrix can be found is called an invertible matrix.

Finding the Inverse Matrix by Gaussian Elimination of Unknowns

The first step to find the inverse matrix by Gaussian elimination is to assign to the matrix A identity matrix of the same order, separating them with a vertical bar. We get a dual matrix. Multiply both parts of this matrix by , then we get

Algorithm for finding the inverse matrix by the Gaussian elimination of unknowns

1. To the matrix A assign an identity matrix of the same order.

2. Transform the resulting dual matrix so that the identity matrix is obtained in its left part, then the inverse matrix will automatically be obtained in the right part in place of the identity matrix. Matrix A on the left side is converted to the identity matrix by elementary transformations of the matrix.

2. If in the process of matrix transformation A into the identity matrix in any row or in any column there will be only zeros, then the determinant of the matrix is equal to zero, and, therefore, the matrix A will be degenerate, and it has no inverse matrix. In this case, further finding of the inverse matrix stops.

Example 2 For matrix

find the inverse matrix.

and we will transform it so that the identity matrix is obtained on the left side. Let's start the transformation.

Multiply the first row of the left and right matrix by (-3) and add it to the second row, and then multiply the first row by (-4) and add it to the third row, then we get

So that, if possible, there are no fractional numbers during subsequent transformations, we will first create a unit in the second row on the left side of the dual matrix. To do this, multiply the second row by 2 and subtract the third row from it, then we get

Let's add the first row to the second, and then multiply the second row by (-9) and add it to the third row. Then we get

Divide the third row by 8, then

Multiply the third row by 2 and add it to the second row. It turns out:

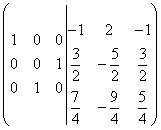Swapping the places of the second and third lines, then we finally get:

We see that the identity matrix is obtained on the left side, therefore, the inverse matrix is obtained on the right side. In this way:

You can check the correctness of the calculations by multiplying the original matrix by the found inverse matrix:

The result should be an inverse matrix.

online calculator for finding the inverse matrix .

Example 3 For matrix

find the inverse matrix.

Solution. Compiling a dual matrix

and we will transform it.

We multiply the first row by 3, and the second by 2, and subtract from the second, and then we multiply the first row by 5, and the third by 2 and subtract from the third row, then we get

We multiply the first row by 2 and add it to the second, and then subtract the second from the third row, then we get

We see that in the third line on the left side, all elements turned out to be equal to zero. Therefore, the matrix is degenerate and has no inverse matrix. We stop further finding of the reverse maria.

You can check the solution with