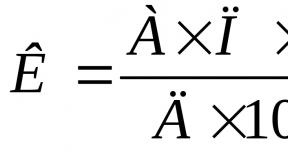The random variable is called distributed according to the normal (Gaussian) law with parameters a and () , if the probability distribution density has the form

A value distributed according to the normal law always has an infinite number of possible values, so it is convenient to depict it graphically, using a distribution density graph. According to the formula

the probability that a random variable will take a value from the interval is equal to the area under the graph of the function on this interval (the geometric meaning of a certain integral). The function under consideration is non-negative and continuous. The graph of a function has the form of a bell and is called a Gaussian curve or a normal curve.

The figure shows several curves of the distribution density of a random variable specified according to the normal law.

All curves have one maximum point, from which the curves decrease to the right and to the left. The maximum is reached at and is equal to .

The curves are symmetrical with respect to a vertical straight line drawn through the highest point. The subplot area of ​​each curve is 1.

The difference between individual distribution curves lies only in the fact that the total area of ​​the subplot, which is the same for all curves, is distributed in different ways between different sections. The main part of the area of ​​the subgraph of any curve is concentrated in the immediate vicinity of the most probable value, and this value is different for all three curves. For different values ​​and a various normal laws and various graphs of the density of the distribution function are obtained.

Theoretical studies have shown that most of the random variables encountered in practice have a normal distribution law. According to this law, the speed of gas molecules, the weight of newborns, the size of clothes and shoes of the population of the country, and many other random events of a physical and biological nature are distributed. For the first time this pattern was noticed and theoretically substantiated by A. De Moivre.

For , the function coincides with the function , which was already discussed in the local limit theorem of Moivre–Laplace. The probability density of a normal distribution is easy expressed through:

For such values ​​of the parameters, the normal law is called main .

The distribution function for the normalized density is called Laplace function and denoted Φ(x). We have also already met this function.

The Laplace function does not depend on specific parameters a and σ. For the Laplace function, using approximate integration methods, tables of values ​​on the interval were compiled with varying degrees of accuracy. It is obvious that the Laplace function is odd, therefore, there is no need to put its values ​​in the table for negative .

For a random variable distributed according to the normal law with parameters a and , the mathematical expectation and variance are calculated by the formulas: , . The standard deviation is equal to .

The probability that a normally distributed quantity takes a value from the interval is equal to

where is the Laplace function introduced in the integral limit theorem.

Often in problems it is required to calculate the probability that the deviation of a normally distributed random variable X from its mathematical expectation in absolute value does not exceed some value , i.e. calculate the probability. Applying formula (19.2), we have:

In conclusion, we present one important consequence of formula (19.3). Let's put in this formula. Then , i.e. the probability that the absolute value of the deviation X from its mathematical expectation will not exceed , equal to 99.73%. In practice, such an event can be considered reliable. This is the essence of the three sigma rule.

Three sigma rule. If a random variable is normally distributed, then the absolute value of its deviation from the mathematical expectation practically does not exceed three times the standard deviation.

Examples of random variables distributed according to the normal law are the height of a person, the mass of the caught fish of the same species. Normal distribution means the following : there are values ​​​​of human height, the mass of fish of the same species, which on an intuitive level are perceived as "normal" (and in fact - averaged), and they are much more common in a sufficiently large sample than those that differ up or down.

The normal probability distribution of a continuous random variable (sometimes the Gaussian distribution) can be called bell-shaped due to the fact that the density function of this distribution, which is symmetric about the mean, is very similar to the cut of a bell (red curve in the figure above).

The probability of meeting certain values ​​in the sample is equal to the area of ​​​​the figure under the curve, and in the case of a normal distribution, we see that under the top of the "bell", which corresponds to values ​​tending to the average, the area, and hence the probability, is greater than under the edges. Thus, we get the same thing that has already been said: the probability of meeting a person of "normal" height, catching a fish of "normal" weight is higher than for values ​​that differ up or down. In very many cases of practice, measurement errors are distributed according to a law close to normal.

Let's stop again at the figure at the beginning of the lesson, which shows the density function of the normal distribution. The graph of this function was obtained by calculating some data sample in the software package STATISTICS. On it, the histogram columns represent intervals of sample values ​​whose distribution is close (or, as they say in statistics, do not differ significantly from) to the normal distribution density function graph itself, which is a red curve. The graph shows that this curve is indeed bell-shaped.

The normal distribution is valuable in many ways because knowing only the mean of a continuous random variable and the standard deviation, you can calculate any probability associated with that variable.

The normal distribution has the added benefit of being one of the easiest to use statistical criteria used to test statistical hypotheses - Student's t-test- can be used only in the case when the sample data obey the normal distribution law.

The density function of the normal distribution of a continuous random variable can be found using the formula:

,

where x- value of the variable, - mean value, - standard deviation, e\u003d 2.71828 ... - the base of the natural logarithm, \u003d 3.1416 ...

Properties of the normal distribution density function

Changes in the mean move the bell curve in the direction of the axis Ox. If it increases, the curve moves to the right, if it decreases, then to the left.

If the standard deviation changes, then the height of the curve vertex changes. When the standard deviation increases, the top of the curve is higher, when it decreases, it is lower.

The probability that the value of a normally distributed random variable will fall within a given interval

Already in this paragraph, we will begin to solve practical problems, the meaning of which is indicated in the title. Let us analyze what possibilities the theory provides for solving problems. The starting concept for calculating the probability of a normally distributed random variable falling into a given interval is the integral function of the normal distribution.

Integral normal distribution function:

.

However, it is problematic to obtain tables for every possible combination of mean and standard deviation. Therefore, one of the simple ways to calculate the probability of a normally distributed random variable falling into a given interval is to use probability tables for a standardized normal distribution.

A normal distribution is called a standardized or normalized distribution., whose mean value is , and the standard deviation is .

Density function of the standardized normal distribution:

.

Cumulative function of the standardized normal distribution:

.

The figure below shows the integral function of the standardized normal distribution, the graph of which was obtained by calculating some data sample in the software package STATISTICS. The graph itself is a red curve, and the sample values ​​are approaching it.

To enlarge the picture, you can click on it with the left mouse button.

Standardizing a random variable means moving from the original units used in the task to standardized units. Standardization is performed according to the formula

In practice, all possible values ​​of a random variable are often not known, so the values ​​of the mean and standard deviation cannot be accurately determined. They are replaced by the arithmetic mean of the observations and the standard deviation s. Value z expresses the deviations of the values ​​of a random variable from the arithmetic mean when measuring standard deviations.

Open interval

The probability table for the standardized normal distribution, which is available in almost any book on statistics, contains the probabilities that a random variable having a standard normal distribution Z takes on a value less than a certain number z. That is, it will fall into the open interval from minus infinity to z. For example, the probability that the value Z less than 1.5 is equal to 0.93319.

Example 1 The company manufactures parts that have a normally distributed lifetime with a mean of 1000 and a standard deviation of 200 hours.

For a randomly selected part, calculate the probability that its service life will be at least 900 hours.

Solution. Let's introduce the first notation:

The desired probability.

The values ​​of the random variable are in the open interval. But we can calculate the probability that a random variable will take a value less than a given value, and according to the condition of the problem, it is required to find an equal or greater value than a given one. This is the other part of the space under the bell curve. Therefore, in order to find the desired probability, it is necessary to subtract from one the mentioned probability that the random variable will take a value less than the specified 900:

Now the random variable needs to be standardized.

We continue to introduce the notation:

z = (X ≤ 900) ;

x= 900 - given value of a random variable;

μ = 1000 - average value;

σ = 200 - standard deviation.

Based on these data, we obtain the conditions of the problem:

.

According to the tables of a standardized random variable (interval boundary) z= −0.5 corresponds to the probability 0.30854. Subtract it from unity and get what is required in the condition of the problem:

So, the probability that the life of the part will be at least 900 hours is 69%.

This probability can be obtained using the MS Excel function NORM.DIST (the value of the integral value is 1):

P(X≥900) = 1 - P(X≤900) = 1 - NORM.DIST(900; 1000; 200; 1) = 1 - 0.3085 = 0.6915.

About calculations in MS Excel - in one of the subsequent paragraphs of this lesson.

Example 2 In some city, the average annual family income is a normally distributed random variable with a mean value of 300,000 and a standard deviation of 50,000. It is known that the income of 40% of families is less than the value A. Find value A.

Solution. In this problem, 40% is nothing more than the probability that a random variable will take a value from an open interval that is less than a certain value, indicated by the letter A.

To find the value A, we first compose the integral function:

According to the task

μ = 300000 - average value;

σ = 50000 - standard deviation;

x = A is the value to be found.

Making up equality

.

According to the statistical tables, we find that the probability of 0.40 corresponds to the value of the interval boundary z = −0,25 .

Therefore, we make the equality

and find its solution:

A = 287300 .

Answer: income of 40% of families is less than 287300.

Closed interval

In many problems, it is required to find the probability that a normally distributed random variable takes a value in the interval from z 1 to z 2. That is, it will fall into the closed interval. To solve such problems, it is necessary to find in the table the probabilities corresponding to the boundaries of the interval, and then find the difference between these probabilities. This requires subtracting the smaller value from the larger one. Examples for solving these common problems are as follows, and it is proposed to solve them yourself, and then you can see the correct solutions and answers.

Example 3 The profit of an enterprise for a certain period is a random variable subject to the normal distribution law with an average value of 0.5 million c.u. and a standard deviation of 0.354. Determine, with an accuracy of two decimal places, the probability that the profit of the enterprise will be from 0.4 to 0.6 c.u.

Example 4 The length of the manufactured part is a random variable distributed according to the normal law with parameters μ =10 and σ =0.071 . Find, with an accuracy of two decimal places, the probability of marriage if the allowable dimensions of the part should be 10 ± 0.05.

Hint: in this problem, in addition to finding the probability of a random variable falling into a closed interval (the probability of obtaining a non-defective part), one more action is required.

allows you to determine the probability that the standardized value Z not less -z and no more +z, where z- an arbitrarily chosen value of a standardized random variable.

An Approximate Method for Checking the Normality of a Distribution

An approximate method for checking the normality of the distribution of sample values ​​is based on the following property of a normal distribution: skewness β 1 and kurtosis coefficient β 2 zero.

Asymmetry coefficient β 1 numerically characterizes the symmetry of the empirical distribution with respect to the mean. If the skewness is equal to zero, then the arithmetric mean, median and mode are equal: and the distribution density curve is symmetrical about the mean. If the coefficient of asymmetry is less than zero (β 1 < 0 ), then the arithmetic mean is less than the median, and the median, in turn, is less than the mode () and the curve is shifted to the right (compared to the normal distribution). If the coefficient of asymmetry is greater than zero (β 1 > 0 ), then the arithmetic mean is greater than the median, and the median, in turn, is greater than the mode () and the curve is shifted to the left (compared to the normal distribution).

Kurtosis coefficient β 2 characterizes the concentration of the empirical distribution around the arithmetic mean in the direction of the axis Oy and the degree of peaking of the distribution density curve. If the kurtosis coefficient is greater than zero, then the curve is more elongated (compared to the normal distribution) along the axis Oy(the graph is more pointed). If the kurtosis coefficient is less than zero, then the curve is more flattened (compared to a normal distribution) along the axis Oy(the graph is more obtuse).

The skewness coefficient can be calculated using the MS Excel function SKRS. If you are checking one array of data, then you need to enter a range of data in one "Number" box.

The coefficient of kurtosis can be calculated using the MS Excel function kurtosis. When checking one data array, it is also enough to enter the data range in one "Number" box.

So, as we already know, with a normal distribution, the skewness and kurtosis coefficients are equal to zero. But what if we got skewness coefficients equal to -0.14, 0.22, 0.43, and kurtosis coefficients equal to 0.17, -0.31, 0.55? The question is quite fair, since in practice we deal only with approximate, selective values ​​of asymmetry and kurtosis, which are subject to some inevitable, uncontrollable scatter. Therefore, it is impossible to require strict equality of these coefficients to zero, they should only be sufficiently close to zero. But what does enough mean?

It is required to compare the received empirical values ​​with admissible values. To do this, you need to check the following inequalities (compare the values ​​of the coefficients modulo with the critical values ​​- the boundaries of the hypothesis testing area).

For the asymmetry coefficient β 1 .

In probability theory, a fairly large number of various distribution laws are considered. For solving problems related to the construction of control charts, only some of them are of interest. The most important of them is normal distribution law, which is used to build control charts used in quantitative control, i.e. when we are dealing with a continuous random variable. The normal distribution law occupies a special position among other distribution laws. This is explained by the fact that, firstly, it is most often encountered in practice, and, secondly, it is the limiting law, to which other laws of distribution approach under very often encountered typical conditions. As for the second circumstance, it has been proven in probability theory that the sum of a sufficiently large number of independent (or weakly dependent) random variables subject to any distribution laws (subject to certain very non-rigid restrictions) approximately obeys the normal law, and this is fulfilled the more accurately the greater the number of random variables summed up. Most of the random variables encountered in practice, such as, for example, measurement errors, can be represented as the sum of a very large number of relatively small terms - elementary errors, each of which is caused by the action of a separate cause independent of the others. The normal law occurs when the random variable X is the result of a large number of different factors. Each factor separately by the value X influences slightly, and it is impossible to specify which one influences to a greater extent than the others.

Normal distribution(Laplace–Gauss distribution) is the probability distribution of a continuous random variable X such that the probability distribution density at - ¥<х< + ¥ принимает действительное значение:

exp (3)

That is, the normal distribution is characterized by two parameters m and s, where m is the mathematical expectation; s is the standard deviation of the normal distribution.

s value 2 is the variance of the normal distribution.

The mathematical expectation m characterizes the position of the distribution center, and the standard deviation s (RMS) is a dispersion characteristic (Fig. 3).

f(x) f(x)

Figure 3 - Density functions of the normal distribution with:

a) different mathematical expectations m; b) different RMS s.

Thus, the value μ is determined by the position of the distribution curve on the x-axis. Dimension μ - the same as the dimension of the random variable X. As the mathematical expectation increases, both functions move parallel to the right. With decreasing variance s 2 the density becomes more and more concentrated around m, while the distribution function becomes more and more steep.

The value of σ determines the shape of the distribution curve. Since the area under the distribution curve must always remain equal to unity, as σ increases, the distribution curve becomes flatter. On fig. 3.1 shows three curves for different σ: σ1 = 0.5; σ2 = 1.0; σ3 = 2.0.

Figure 3.1 - Density functions of the normal distribution with different RMS s .

The distribution function (integral function) has the form (Fig. 4):

(4)

Figure 4 - Integral (a) and differential (b) normal distribution functions

Of particular importance is the linear transformation of a normally distributed random variable X, after which a random variable is obtained Z with mathematical expectation 0 and variance 1. Such a transformation is called normalization:

It can be done for every random variable. Normalization allows all possible variants of the normal distribution to be reduced to one case: m = 0, s = 1.

The normal distribution with m = 0, s = 1 is called normalized normal distribution (standardized).

standard normal distribution(standard Laplace-Gauss distribution or normalized normal distribution) is the probability distribution of a standardized normal random variable Z, the distribution density of which is equal to:

at - ¥<z< + ¥

Function values Ф(z) is determined by the formula:

(7)

Function values Ф(z) and density f(z) normalized normal distribution are calculated and summarized in tables (tabulated). The table is compiled only for positive values z that's why:

F (–z) = 1–Ф (z) (8)

Using these tables, one can determine not only the values ​​of the function and density of the normalized normal distribution for a given z, but also the values ​​of the general normal distribution function, since:

; (9)

. 10)

In many problems related to normally distributed random variables, it is necessary to determine the probability of hitting a random variable X, subject to the normal law with parameters m and s, to a certain area. Such a site can be, for example, a tolerance field for a parameter from the upper value U to the bottom L.

The probability of falling into the interval from X 1 to X 2 can be determined by the formula:

Thus, the probability of hitting a random variable (parameter value) X in the tolerance field is determined by the formula

The normal distribution is the most common type of distribution. It is encountered in the analysis of measurement errors, the control of technological processes and regimes, as well as in the analysis and prediction of various phenomena in biology, medicine and other fields of knowledge.

The term "normal distribution" is used in a conditional sense as generally accepted in the literature, although not entirely successful. Thus, the assertion that a certain attribute obeys the normal distribution law does not mean at all the existence of any unshakable norms that supposedly underlie the phenomenon, the reflection of which is the attribute in question, and the submission to other distribution laws does not mean some kind of abnormality of this phenomenon.

The main feature of the normal distribution is that it is the limit to which other distributions approach. The normal distribution was first discovered by Moivre in 1733. Only continuous random variables obey the normal law. The density of the normal distribution law has the form .

The mathematical expectation for the normal distribution law is . The dispersion is .

Basic properties of the normal distribution.

1. The distribution density function is defined on the entire real axis Oh , that is, each value X corresponds to a well-defined value of the function.

2. For all values X (both positive and negative) the density function takes positive values, that is, the normal curve is located above the axis Oh .

3. Limit of the density function with an unlimited increase X equals zero, .

4. The density function of the normal distribution at the point has a maximum.

5. The graph of the density function is symmetrical about a straight line.

6. The distribution curve has two inflection points with coordinates and .

7. The mode and median of the normal distribution coincide with the mathematical expectation a .

8. The shape of the normal curve does not change when the parameter is changed a .

9. The coefficients of skewness and kurtosis of the normal distribution are equal to zero.

The importance of calculating these coefficients for empirical distribution series is obvious, since they characterize the skewness and steepness of the given series compared to the normal one.

The probability of falling into the interval is found by the formula , where is an odd tabulated function.

Let's determine the probability that a normally distributed random variable deviates from its mathematical expectation by a value less than , that is, we find the probability of the inequality , or the probability of double inequality . Substituting into the formula, we get

Expressing the deviation of a random variable X in fractions of the standard deviation, that is, putting in the last equality, we get .

Then for , we get

when we get ,

when we receive .

It follows from the last inequality that practically the scattering of a normally distributed random variable lies in the section . The probability that a random variable will not fall into this area is very small, namely, it is equal to 0.0027, that is, this event can occur only in three cases out of 1000. Such events can be considered almost impossible. Based on the above reasoning, three sigma rule, which is formulated as follows: if a random variable has a normal distribution, then the deviation of this value from the mathematical expectation in absolute value does not exceed three times the standard deviation.

Example 28 . A part made by an automatic machine is considered fit if the deviation of its controlled size from the design one does not exceed 10 mm. Random deviations of the controlled size from the design size are subject to the normal distribution law with standard deviation mm and mathematical expectation. What percentage of good parts does the machine produce?

Solution. Consider a random variable X - deviation of the size from the design. The part will be recognized as fit if the random variable belongs to the interval . The probability of manufacturing a suitable part is found by the formula . Therefore, the percentage of good parts produced by the machine is 95.44%.

Binomial distribution

Binomial is the probability distribution of occurrence m number of events in P independent tests, in each of which the probability of occurrence of an event is constant and equal to R . The probability of the possible number of occurrences of an event is calculated by the Bernoulli formula: ,

where . Permanent P and R , included in this expression, the parameters of the binomial law. The binomial distribution describes the probability distribution of a discrete random variable.

Basic numerical characteristics of the binomial distribution. The mathematical expectation is . The dispersion is . The skewness and kurtosis coefficients are equal to and . With an unlimited increase in the number of trials BUT and E tend to zero, therefore, we can assume that the binomial distribution converges to the normal one with increasing number of trials.

Example 29 . Independent tests are performed with the same probability of occurrence of the event BUT in every test. Find the probability of an event occurring BUT in one trial if the variance in the number of appearances across three trials is 0.63.

Solution. For the binomial distribution . Substitute the values, we get from here or then and .

Poisson distribution

Law of distribution of rare phenomena

The Poisson distribution describes the number of events m , occurring in equal time intervals, provided that the events occur independently of each other with a constant average intensity. At the same time, the number of trials P is large, and the probability of an event occurring in each trial R small. Therefore, the Poisson distribution is called the law of rare phenomena or the simplest flow. The parameter of the Poisson distribution is the value characterizing the intensity of occurrence of events in P tests. Poisson distribution formula.

The Poisson distribution well describes the number of claims for the payment of insurance sums per year, the number of calls received by the telephone exchange in a certain time, the number of element failures during reliability testing, the number of defective products, and so on.

Basic numerical characteristics for the Poisson distribution. The mathematical expectation is equal to the variance and is equal to a . That is . This is a distinctive feature of this distribution. The skewness and kurtosis coefficients are respectively equal to .

Example 30 . The average number of payments of sums insured per day is two. Find the probability that in five days you will have to pay: 1) 6 sums insured; 2) less than six amounts; 3) not less than six.distribution.

This distribution is often observed when studying the service life of various devices, the uptime of individual elements, parts of the system and the system as a whole, when considering random time intervals between the occurrence of two successive rare events.

The density of the exponential distribution is determined by the parameter , which is called failure rate. This term is associated with a specific area of ​​application - the theory of reliability.

The expression for the integral function of the exponential distribution can be found using the properties of the differential function:

Mathematical expectation of the exponential distribution, variance, standard deviation. Thus, it is typical for this distribution that the standard deviation is numerically equal to the mathematical expectation. For any value of the parameter, the skewness and kurtosis coefficients are constant values.

Example 31 . The average operating time of the TV before the first failure is 500 hours. Find the probability that a TV set chosen at random will operate without breakdowns for more than 1000 hours.

Solution. Since the average time to first failure is 500, then . We find the desired probability by the formula .

Random if, as a result of experience, it can take on real values ​​with certain probabilities. The most complete, exhaustive characteristic of a random variable is the law of distribution. The distribution law is a function (table, graph, formula) that allows you to determine the probability that a random variable X takes a certain value xi or falls into a certain interval. If a random variable has a given distribution law, then it is said that it is distributed according to this law or obeys this distribution law.

Each distribution law is a function that completely describes a random variable from a probabilistic point of view. In practice, the probability distribution of a random variable X often has to be judged only by test results.

Normal distribution

Normal distribution, also called the Gaussian distribution, is a probability distribution that plays a crucial role in many fields of knowledge, especially in physics. A physical quantity obeys a normal distribution when it is influenced by a huge number of random noises. It is clear that this situation is extremely common, so we can say that of all distributions, it is the normal distribution that most often occurs in nature - hence one of its names came from.

The normal distribution depends on two parameters - displacement and scale, that is, from a mathematical point of view, it is not one distribution, but a whole family of them. The parameter values ​​correspond to the mean (mathematical expectation) and spread (standard deviation) values.

The standard normal distribution is a normal distribution with mean 0 and standard deviation 1.

Asymmetry coefficient

The skewness coefficient is positive if the right tail of the distribution is longer than the left, and negative otherwise.

If the distribution is symmetrical with respect to the mathematical expectation, then its skewness coefficient is equal to zero.

The sample skewness coefficient is used to test the distribution for symmetry, as well as for a rough preliminary test for normality. It allows you to reject, but does not allow you to accept the hypothesis of normality.

Kurtosis coefficient

The coefficient of kurtosis (coefficient of sharpness) is a measure of the sharpness of the peak of the distribution of a random variable.

"Minus three" at the end of the formula is introduced so that the coefficient of kurtosis of the normal distribution is equal to zero. It is positive if the peak of the distribution near the expected value is sharp, and negative if the peak is smooth.

Moments of a random variable

The moment of a random variable is a numerical characteristic of the distribution of a given random variable.