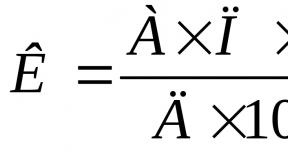Asymmetry and kurtosis of the distribution of a random variable.

090309-matmethod.txt

asymmetric characteristics.

The main measure of asymmetry is the coefficient of asymmetry. That is, the degree of deviation of the frequency distribution graph from the symmetrical form relative to the average value. It is denoted by the letter A with index s and is calculated according to the formula (Fig. 8). The asymmetry coefficient changes from minus infinity to plus infinity. Asymmetry is left-sided (positive), when the coefficient is greater than zero - As> 0 and right-sided (negative) - As<0. При левосторонней ассиметрии чаще встречаются значения ниже среднего арифметического. При правой, соответственно чаще всего встречаются значения, превосходящие среднее арифметическое. Для симметричных распределений коэффициент ассиметрии равен нулю, а мода, медиана и среднее арифметическое значение совпадают между собой.

characteristics of excess.

It characterizes its coefficient of kurtosis (or sharpness) - it is calculated by the formula.

The peaked distribution is characterized by positive kurtosis, the flat-topped distribution is negative, and the mid-topped distribution has zero kurtosis.

firstly, Secondly,

If you-(usually - interval).

Graphical way(Q- Q Plots, R-RPlots).

where N- sample size.

Properties of the normal distribution of a random variable.

090309-matmethod.txt

Normal distribution.

The normal distribution is characterized by the fact that the extreme values ​​of the signs are relatively rare, close to the arithmetic mean - relatively often. The normal distribution curve is bell-shaped. This is a unimodal distribution, the values ​​of the median, mode and arithmetic mean of which coincide with each other, the coefficients of asymmetry and kurtosis lie in the range from zero to two (permissible), but ideally equal to zero.

Since the second half of the 19th century, measuring and computational methods in psychology have been developed on the basis of the following principle. If indievisual variability of a certain property is a consequence of the action of a multitude of reasons, then the frequency distribution for the whole variety of manifestationsof this property in the general population corresponds to the normal curvedistribution. This is the law of normal distribution.

The law of normal distribution has a number of very important consequences, which we will refer to more than once. Now we note that if, when studying a certain property, we measured it on a sample of subjects and received a distribution that differed from the normal one, then this means that either the sample is not representative of the general population, or the measurements were not made in a scale of equal intervals.

To
Each psychological (or, more broadly, biological) property has its own distribution in the general population. Most often it is normal and is characterized by its parameters: average (M) and standard deviation (o). Only these two values ​​distinguish from each other an infinite number of normal curves, of the same shape, given by equation (5.1). The average sets the position of the curve on the real axis and acts as some initial, normative value of measurement. The standard deviation sets the width of this curve, depends on the units of measurement and acts as measurement scale(Fig. 5.3).

Figure 5.3. A family of normal curves, the 1st distribution differs from the 2nd by the standard deviation (σ 1< σ 2), 2-е от 3-го средним арифметическим (M 2 < M 3)

The entire variety of normal distributions can be reduced to a single curve if the ^-transformation (according to formula 4.8) is applied to all possible measurements of properties. Then each property will have a mean of 0 and a standard deviation of 1. In fig. 5.4 a graph of the normal distribution is plotted for M= 0 and a = 1. That's what it isunit Normal Distribution, cat-swarm is used as a standard - reference. Consider it important properties.

The unit of measure for a unit normal distribution is the standard deviation.

The curve approaches the Z-axis at the edges asymptotically - never touching it.

The curve is symmetrical with respect to M=0. Its skewness and kurtosis are zero.

The curve has a characteristic bend: the inflection point lies exactly one σ away from M.

The area between the curve and the Z axis is 1.

The last property explains the name singular normal distribution and is extremely important. Thanks to this property the area under the curve is interpreted as a probability, or relativefrequency. Indeed, the entire area under the curve corresponds to the probability that the feature will take on any value from the entire range of its variability (from -oo to +oo). The area under the unit normal curve to the left or right of the zero point is 0.5. This corresponds to the fact that half of the general population has a feature value greater than 0, and half is less than 0. The relative frequency of occurrence in the general population of feature values ​​in the range from Z\ before Zi equal to the area under the curve lying between the corresponding points. Note again that any normal distribution can be reduced to a unit normal distribution by z- transformations.

So, the most important common property of different normal distribution curves is the same proportion of the area under the curve between the same two values ​​of the trait, expressed in units of standard deviation.

It is useful to remember that for any normal distribution, there are the following correspondences between the ranges of values ​​and the area under the curve:

The unit normal distribution establishes a clear relationship between the standard deviation and the relative number of cases in the general population for any normal distribution. For example, knowing the properties of a unit normal distribution, we can answer the following questions. What proportion of the general population has the severity of the property from - \about up to +1o? Or what is the probability that a randomly selected representative of the general population will have the severity of the property by For exceeding the average value? In the first case, the answer will be 68.26% of the entire population, since from - 1 to +1 contains 0.6826 of the area of ​​​​a unit normal distribution. In the second case, the answer is: (100-99.72)/2 = 0.14%.

There is a special table that allows you to determine the area under the curve to the right of any positive z (Attachment 1). Using it, you can determine the probability of occurrence of feature values ​​from any range. This is widely used in interpreting test data.

Despite the initial postulate, according to which properties in the general population have a normal distribution, real data obtained from a sample are rarely normally distributed. Moreover, many methods have been developed to analyze data without any assumption about the nature of their distribution, both in the sample and in the general population. These circumstances sometimes lead to the false belief that the normal distribution is an empty mathematical abstraction that has nothing to do with psychology. Nevertheless, as we shall see later, there are at least three important aspects of the normal distribution that can be pointed out:

Development of test scales.

Checking the normality of the sample distribution to make a decision
decisions about the scale in which the trait is measured - in metric or
row.

Statistical testing of hypotheses, in particular - in determining risk
making the wrong decision.

Standard normal distribution. Distribution standardization.

(Full question #12 + about standardization see below)

091208-matmethodody.txt

standardization psychodiagnostic methods (more on this in question #17)

General population and sample.

091208-matmethodody.txt

General aggregates.

Any psychodiagnostic technique is designed to examine some large category of individuals. This set is called the general population.

To determine the degree of expression of a particular property in one specific person, you need to know how this quality is distributed throughout the general population. It is practically impossible to examine the general population, therefore, they resort to extracting a sample from the general population, that is, some representative part of the general population. It is this representativeness (in other words, it is called "representativeness") that is the main requirement for the sample. It is impossible to ensure an absolutely exact match of this requirement. You can only get closer to the ideal with the help of some methods. The main ones are 1) randomness and 2) simulation.

1) Random sampling assumes that the subjects will fall into it randomly. Measures are being taken to exclude the appearance of any patterns.

2) When modeling, first those properties are selected that can affect the test results. Usually these are demographic characteristics, within which gradations are distinguished: age intervals, levels of education, etc. Based on these data, a matrix model of the general population is built.

Typically, methods are standardized on a sample of 200 to 800 people.

The standardization of psychodiagnostic methods is the procedure for obtaining a scale that allows you to compare an individual test result with the results of a large group.

Research usually begins with some assumption, requiring verification with the involvement of facts. This assumption - a hypothesis - is formulated in relation to the connection of phenomena or properties in a certain set of objects.

To test such assumptions on the facts, it is necessary to measure the corresponding properties of their carriers. But it is impossible to measure anxiety in all women and men, just as it is impossible to measure aggressiveness in all adolescents. Therefore, when conducting a study, they are limited to only a relatively small group of representatives of the relevant populations of people.

Population- this is the whole set of objects in relation to which a research hypothesis is formulated.

In the first example, such populations are all men and all women. In the second - all teenagers who watch TV shows containing scenes of violence. General populations, in relation to which the researcher is going to draw conclusions from the results of the study, may be more modest in number.

Thus, the general population is, although not an infinite ps of numbers, but, as a rule, a multitude of potential subjects inaccessible to a continuous study.

Sample- this is a group of objects limited in number (in psychology - subjects, respondents), specially selected from the general population to study its properties. Accordingly, the study of the properties of the general population on a sample is called selective research. Almost all psychological studies are selective, and their conclusions apply to general populations.

Thus, after the hypothesis is formulated and the corresponding general populations are determined, the researcher faces the problem of organizing the sample. The sample should be such that the generalization of the conclusions of the sample study is justified - generalization, their distribution to the general population. The main criteria forvalidity of the study's findings- is the representativeness of the sample andstatistical validity of (empirical) results.

Sample representativeness- in other words, its representativeness is the ability of the sample to represent the studied phenomena quite fully in terms of their variability in the general population.

Of course, only the general population can give a complete picture of the phenomenon under study, in all its range and nuances of variability. Therefore, representativeness is always limited to the extent that the sample is limited. And it is the representativeness of the sample that is the main criterion in determining the boundaries of the generalization of the findings of the study. However, there are techniques to obtain sufficient representativeness of the sample for the researcher. (Question #15 is a continuation of this question)

The main methods of sampling.

With. 13 (20) (Question #14 is a prelude to this question)

The first and main approach is simple random (randomized)selection. It involves ensuring that each member of the population has an equal chance of being included in the sample. Random selection provides the possibility of getting into the sample of the most diverse representatives of the general population. At the same time, special measures are taken to exclude the appearance of any regularity in the selection. And this allows us to hope that in the end, in the sample, the studied property will be represented, if not in all, then in its maximum possible variety.

The second way to ensure representativeness is to stratified random selection, or selection according to the properties of the general population. It involves a preliminary determination of those qualities that may affect the variability of the property being studied (this may be gender, income level or education, etc.). Then the percentage ratio of the number of groups (strata) differing in these qualities in the general population is determined and an identical percentage ratio of the corresponding groups in the sample is provided. Further, in each subgroup of the sample, the subjects are selected according to the principle of simple random selection.

statistical validity, or statistical significance, the results of the study are determined using statistical inference methods. We will consider these methods in detail in the second part of this book. For now, we only note that they impose certain requirements on the number, or sample size.

Unfortunately, there are no strict recommendations on the preliminary determination of the required sample size. Moreover, the researcher usually receives an answer to the question about its necessary and sufficient number too late - only after analyzing the data of an already surveyed sample. However, the most general recommendations can be formulated:

□ The largest sample size is required when developing a diagnostic technique - from 200 to 1000-2500 people.

If it is necessary to compare 2 samples, their total number should
be at least 50 people; the number of compared samples should
be approximately the same.

P If the relationship between any properties is being studied, then the sample size should be at least 30-35 people.

□ The more variability of the studied property, the more should be
sample size. Therefore, the variability can be reduced by increasing
homogeneity of the sample, for example, by sex, age, etc. At the same time,
Naturally, the possibilities of generalization of conclusions are reduced.

Dependent and independent samples. A typical research situation is when a property of interest to the researcher is studied on two or more samples for the purpose of their further comparison. These samples may be in different proportions - depending on the procedure for their organization. Independentmy samples are characterized by the fact that the probability of selection of any subject of one sample does not depend on the selection of any of the subjects of another sample. Against, dependent samples are characterized by the fact that each subject of one sample is matched by a certain criterion with a subject from another sample.

In the general case, dependent samples involve a pairwise selection of subjects in the compared samples, and independent samples - an independent selection of subjects.

It should be noted that the cases of “partially dependent” (or “partially independent”) samples are not allowed: this violates their representativeness in an unpredictable way.

In conclusion, we note that two paradigms of psychological research can be distinguished. So-called R-methodology involves the study of the variability of a certain property (psychological) under the influence of some influence, factor or other property. The sample is a lot test subjects . Another approach Q-methodology, involves the study of the variability of the subject (single) under the influence of various stimuli (conditions, situations, etc.). It corresponds to the situation when sample is there are many incentives .

Checking the sample for outliers.

To test for normality, various procedures are used to find out whether the sample distribution of the measured variable differs from the normal one. The need for such a comparison arises when we doubt in which scale the feature is presented - in ordinal or metric. And such doubts arise very often, since, as a rule, we do not know in advance on which scale it will be possible to measure the property under study (excluding, of course, cases of a clearly nominative measurement).

The importance of determining in which scale a trait is measured cannot be overestimated, for at least two reasons. Depends on, firstly, completeness of taking into account the initial empirical information (in particular, about individual differences), Secondly, availability of many methods of data analysis. If the researcher decides to measure on an ordinal scale, then the inevitable subsequent ranking leads to the loss of some of the initial information about the differences between the subjects, the studied groups, about the relationship between the signs, etc. In addition, metric data allow the use a significantly wider range of analysis methods and, as a result, to make the conclusions of the study deeper and more meaningful.

The most weighty argument in favor of the fact that the trait is measured on a metric scale is the compliance of the sample distribution with the normal one. This is a consequence of the law of normal distribution. If you-the barrage distribution does not differ from the normal one, this means thatthe measured property was reflected in the metric scale(usually - interval).

There are many different ways of testing normality, of which we will briefly describe only a few, assuming that these tests will be performed by the reader using computer programs.

Graphical way(Q- Q Plots, R-RPlots). Build either quantile graphs or graphs of accumulated frequencies. Quantile plots (Q- Q Plots) are constructed in the following way. First, the empirical values ​​of the trait under study are determined, corresponding to the 5th, 10th, ..., 95th percentile. The z-scores (theoretical) are then determined from the normal distribution table for each of these percentiles. The two series of numbers obtained set the coordinates of the points on the graph: the empirical values ​​of the feature are plotted on the abscissa axis, and the theoretical values ​​corresponding to them are plotted on the ordinate axis. For a normal distribution, all points will bepress on or near one straight line. The greater the distance from the points to the straight line, the less the distribution corresponds to the normal one. Graphs of accumulated frequencies (Р-РPlots) are built in a similar way. On the x-axis, at regular intervals, the values ​​​​of the accumulated relative frequencies are plotted, for example, 0.05; 0.1; ...; 0.95. Next, the empirical values ​​of the trait under study are determined, corresponding to each value of the accumulated frequency, which are recalculated into z-values. Bythe normal distribution table determines the theoretical accumulationfixed frequencies (area under the curve) for each of the computed r-values ​​that are plotted on the y-axis. If the distributioncorresponds to normal, the points obtained on the graph lie on the samestraight.

Criteria of asymmetry and kurtosis. These criteria determine the acceptable degree of deviation of the empirical values ​​of skewness and kurtosis from zero values ​​corresponding to the normal distribution. The acceptable degree of deviation is that which makes it possible to consider that these statistics do not differ significantly from the normal parameters. The value of permissible deviations is determined by the so-called standard errors of asymmetry and kurtosis. For the asymmetry formula (4.10), the standard error is determined by the formula:

where N- sample size.

Sample values ​​of skewness and kurtosis are significantly different from zero if they do not exceed the values ​​of their standard errors. This can be considered a sign that the sample distribution corresponds to the normal law. It should be noted that computer programs calculate the indicators of asymmetry, kurtosis and their corresponding standard errors using other, more complex formulas.

Kolmogorov-Smirnov statistical normality criterion is considered the most consistent for determining the degree of correspondence between the empirical distribution and the normal one. It allows you to estimate the probability that a given sample belongs to a population with a normal distribution. If this probability R< 0.05, then this empirical distribution differs significantly from the normal one, and if R> 0.05, then a conclusion is made about the approximate correspondence of this empirical distribution to the normal one.

Causes of deviation from normality. The common reason for the deviation of the form of the sample distribution of a trait from the normal form is most often a feature of the measurement procedure: the scale used may have uneven sensitivity to the measured property in different parts of the range of its variability.

EXAMPLE Let's assume that the severity of some ability is determined by the number of completed tasks in the allotted time. If the tasks are simple or the time is too long, then this measuring procedure will have sufficient sensitivity only in relation to the part of the subjects for whom these tasks are difficult enough. And too much of the test subjects will solve all or almost all tasks. As a result, we get a distribution with a pronounced right-sided asymmetry. You can, of course, subsequently improve the quality of the measurement by empirical normalization, adding more complex tasks or reducing the execution time of a given set of tasks. If we overly complicate the measurement procedure, then the opposite situation will arise, when the majority of the subjects will solve a small number of tasks and the empirical distribution will acquire left-sided asymmetry.

Thus, such deviations from the normal form, such as right- or left-sided asymmetry or too large kurtosis (greater than 0), are associated with the relatively low sensitivity of the measurement procedure in the mode region (tops of the frequency distribution graph).

Consequences of rejection from normality. It should be noted that the problem of obtaining an empirical distribution that strictly corresponds to the normal law is rarely encountered in research practice. Usually such cases are limited to the development of a new measurement procedure or test scale, when empirical or non-linear normalization is applied to "correct" the empirical distribution. Mostcases, compliance or non-compliance with normality is one of themeasured trait, which the researcher must take into account whenchoice of statistical procedures for data analysis.

In the general case, with a significant deviation of the empirical distribution from the normal one, one should abandon the assumption that the sign is measured on a metric scale. But the question remains, what is the measure of the significance of this deviation? In addition, different methods of data analysis have different sensitivity to deviations from normality. Usually, when justifying the prospects of this problem, they cite the principle of R. Fisher, one of the "founding fathers" of modern statistics: "Deviations from normaltype, if only they are not too noticeable, can be found only for painour samples; by themselves they make little difference in the statistical critrii and other issues. For example, with small, but usual samples for psychological research (up to 50 people), the Kolmogorov-Smirnov test is not sensitive enough to determine even very noticeable “by eye” deviations from normality. At the same time, some procedures for analyzing metric data quite allow deviations from the normal distribution (some to a greater extent, others to a lesser extent). In what follows, when presenting the material, we will, if necessary, specify the degree of rigidity of the normality requirement.

Basic rules for the standardization of psychodiagnostic methods.

091208-matmethodody.txt

standardization psychodiagnostic methods called the procedure for obtaining a scale that allows you to compare an individual test result with the results of a large group.

Test scales are developed in order to evaluate an individual test result by comparing it with test norms obtained on a standardization sample. Sample standardization it is specially formed for the development of a test scale - it must be representative of the general population for which it is planned to apply this test. Subsequently, when testing, it is assumed that both the test subject and the standardization sample belong to the same general population.

The starting principle in developing a test scale is the assumption that the property being measured is distributed in the general population in accordance with the normal law. Accordingly, the measurement in the test scale of this property on the standardization sample should also provide a normal distribution. If so, then the test scale is metric - more precisely, equal intervals. If this is not so, then the property could be reflected at best - in the scale of order. Naturally, most standard test scales are metric, which makes it possible to interpret the test results in more detail - taking into account the properties of the normal distribution - and correctly apply any methods of statistical analysis. Thus, the main problem of the standardtization of the test is to develop a scale in which the distributiontest indicators on the standardization sample would correspond tonormal distribution.

Initial test scores are the number of answers to certain test questions, the time or number of tasks solved, etc. They are also called primary, or "raw" scores. The result of standardization are test norms - a table for converting "raw" grades into standard test scales.

There are many standard test scales, the main purpose of which is to present individual test results in a form convenient for interpretation. Some of these scales are shown in Fig. 5.5. Common to them is compliance with the normal distribution, and they differ only in two indicators: the mean value and the scale (standard deviation - o), which determines the fractional scale.

General sequence of standardization(development of test norms - tables for recalculating "raw" grades into standard test ones) is as follows:

the general population is determined for which it is developed
methodology and a representative sample of standardization is formed;

based on the results of applying the primary test version, a distribution is built
determination of "raw" estimates;

check the compliance of the obtained distribution with the normal
horse;

if the distribution of "raw" estimates corresponds to normal,
harassed linear standardization;

if the distribution of "raw" estimates does not correspond to the normal one, then
two options are possible:

before linear standardization, an empirical norm is produced
lysis;

carry out non-linear normalization.

Checking the distribution of "raw" estimates for compliance with the normal law is carried out using special criteria, which we will consider later in this chapter.

Linear standardization lies in the fact that the boundaries of the intervals of "raw" estimates are determined, corresponding to standard test indicators. These limits are calculated by adding (or subtracting from it) the proportions of standard deviations corresponding to the test scale to the average of the "raw" estimates.

Test norms - a table for converting "raw" scores into walls

Using this table of test norms, the individual result (“raw” score) is converted into a wall scale, which allows interpreting the severity of the measured property.

Empirical normalization is used when the distribution of raw scores differs from the normal one. It consists in changing the content of test tasks. For example, if the “raw” assessment is the number of tasks solved by the subjects in the allotted time, and a distribution with right-sided asymmetry is obtained, then this means that too large a proportion of the subjects solves more than half of the tasks. In this case, it is necessary to either add more difficult tasks or reduce the solution time.

Nonlinear normalization is applied if empirical normalization is impossible or undesirable, for example, in terms of time and resources. In this case, the conversion of "raw" estimates into standard ones is carried out by finding the percentile boundaries of groups in the original distribution, corresponding to the percentile boundaries of groups in the normal distribution of the standard scale. Each interval of the standard scale is assigned such an interval of the scale of "raw" assessments, which contains the same percentage of the standardization sample. The values ​​of the shares are determined by the area under the unit normal curve, enclosed between the r-estimates corresponding to this interval of the standard scale.

For example, in order to determine which “raw” score should correspond to the lower boundary of wall 10, you must first find out what r-value this boundary corresponds to (z = 2). Then, using the normal distribution table (Appendix 1), it is necessary to determine what proportion of the area under the normal curve is to the right of this value (0.023). After that, it is determined which value cuts off the 2.3% of the highest values ​​of the "raw" points of the standardization sample. The found value will correspond to the border of 9 and 10 walls.

The outlined foundations of psychodiagnostics allow us to formulate mathematically justified requirements for the test. The test procedure shouldKeep:

description of the standardization sample;

characteristics of the distribution of "raw" scores indicating the average and
standard deviation;

name, description of the standard scale;

test norms - tables for converting "raw" scores into scale ones.

Z-score scale. (???)

091208-matmethodody.txt

The standardized (or standard) deviation is usually denoted by the letter Z. (Fig. 1 in the notebook) Z-scores are obtained.

A special place among normal distributions is occupied by the so-called standard or unit normal distribution. Such a distribution is obtained under the condition that the arithmetic mean is zero, the standard deviation is 1. The normal distribution is convenient because any distribution can be reduced to it by standardization.

The standardization operation is as follows: the arithmetic mean value is subtracted from each individual parameter value. This operation is called centering. And the resulting difference is divided by the value of the standard deviation. This operation is called normalization.

With. 47 (54) (see the figure with scales there)

monitoring2.htm

Thus, if we subtract the result of a particular subject from the average and divide the difference by the standard deviation, then we can express the individual score as a fraction of the standard deviation. Shares obtained in this way in diagnostics are called Z-scores. The Z-score is the basis of any standard scale. The most attractive feature of z-scores is that they characterize the relative position of the result of the subject among all the results of the group, regardless of the mean and standard deviation. In addition, z-scores are unit-free. Thanks to these two properties of z-scores, they can be used to compare results obtained in a variety of ways and on a variety of aspects of a sample of behavior.

Stanine scale
wall scale
T-scale
IQ scale

Scales derived from the Z-score scale.

monitoring2.htm (there is also a good start about standardization and standard deviation)

The disadvantage of the z-scale is that you have to deal with fractional and negative values.. Therefore, it is usually converted to the so-called standard scales, which are more convenient to use. Traditionally and more often than others, such scales are used in diagnostics as:

Stanine scale
wall scale
T-scale
IQ scale

With. 47 (54) (see the figure with scales there)

0028.htm 7. Standardization of the psychological questionnaire

Normalization of testing indicators.

In order for the psychological questionnaire to be used practically, i.e. to make, on the basis of its completion by an arbitrarily taken subject, a forecast of his behavior in new situations (using the validity criteria of this questionnaire), it is necessary to normalize the indicators on a normative sample. Only the use of statistical standards makes it possible to judge an increase or decrease in the severity of a particular psychological quality in a particular subject. Although norms are important for applied psychology, it is easiest to use raw indicators directly for psychological research.

The indicators of a particular subject should be compared with those of an adequate normative group. This is done through some transformation that reveals the status of this individual in relation to this group.

Linear and non-linear transformations of raw scale values. Standard indicators can be obtained both by linear and non-linear transformation of primary indicators. Linear transformations are obtained by subtracting a constant from the primary indicator and further dividing by another constant, therefore, all relationships characteristic of primary indicators also take place for linear ones. The most commonly used z-score (Formula 3).

But due to the fact that the distribution of final scores on a particular scale is often not normal, it is impossible to derive percentiles from these standardized indicators, i.e. estimate how many percent of the subjects received the same indicator as the given subject.

If percentile normalization with wall translation and linear normalization with wall translation give the same wall values, then the distribution is considered normal to within a standard ten.

To achieve comparability of results belonging to distributions of different shapes, a non-linear transformation can be applied.

Normalized standard scores obtained using a non-linear transformation are standard scores corresponding to a distribution that has been transformed so that it becomes normal. To calculate them, special tables are created for converting raw points into standard ones. They give the percentage of cases of various degrees of deviation (in units of σ from the mean). Thus, the mean value, which corresponds to the achievement of 50% of the results of the group, can be equated to 0. The mean value minus the standard deviation can be equated to -1, this new value will be observed in about 16% of the sample, and the value +1 - in about 84% .

work Work of speech therapy groups”; 2. "Compliance ... with sanitary standards in school canteens"; 3. About work Administration of the Voivodeship Special (Correctional) School...

When analyzing variational series, the displacement from the center and the steepness of the distribution are characterized by special indicators. Empirical distributions, as a rule, are shifted from the distribution center to the right or to the left, and are asymmetric. The normal distribution is strictly symmetrical with respect to the arithmetic mean, which is due to the evenness of the function.

Distribution skewness arises due to the fact that some factors act in one direction more strongly than in the other, or the process of development of the phenomenon is such that some reason dominates. In addition, the nature of some phenomena is such that there is an asymmetric distribution.

The simplest measure of skewness is the difference between the arithmetic mean, mode, and median:

To determine the direction and magnitude of the shift (asymmetry) of the distribution, the asymmetry factor , which is a normalized moment of the third order:

As= 3 / 3 , where  3 is the central moment of the third order;  3 - standard deviation cubed. 3 \u003d (m 3 - 3m 1 m 2 + 2m 1 3)k 3.

With left-sided asymmetry asymmetry factor (As<0), при правосторонней (As>0) .

If the top of the distribution is shifted to the left and the right side of the branch is longer than the left side, then this asymmetry is right hand, otherwise left-sided .

The ratio between the mode, median and arithmetic mean in symmetric and asymmetric series allows using a simpler indicator as a measure of asymmetry asymmetry coefficient Pearson :

K a = ( –Mo)/. If K a > 0, then the asymmetry is right-sided, if K a<0, то асимметрия левосторонняя, при К a =0 ряд считается симметричным.

More precisely, the asymmetry can be determined using the central moment of the third order:

, where 3 = (m 3 - 3m 1 m 2 + 2m 1 3)k 3 .

If a > 0, then the asymmetry can be considered significant if < 0,25 асимметрию можно считать не значительной.

To characterize the degree of deviation of a symmetrical distribution from a normal distribution along the ordinate, an indicator of sharpness, the steepness of the distribution, is used, called kurtosis :

Ex = ( 4 / 4) - 3, where:  4 - central moment of the fourth order.

For a normal distribution Ex = 0, i.e.  4 /  4 \u003d 3.  4 \u003d (m 4 - 4m 3 m 1 + 6m 2 m 2 1 - 3 m 4 1) * k 4.

For high-vertex curves, the kurtosis is positive, for low-vertex curves, it is negative (Fig. D.2).

Indicators of kurtosis and skewness are necessary in statistical analysis to determine the heterogeneity of the population, the skewness of the distribution and the proximity of the empirical distribution to the normal law. With significant deviations of the asymmetry and kurtosis indicators from zero, it is impossible to recognize the population as homogeneous, and the distribution close to normal. Comparison of actual curves with theoretical ones makes it possible to substantiate mathematically the obtained statistical results, establish the type and nature of the distribution of socio-economic phenomena, and predict the probability of occurrence of the events under study.

4.7. Justification of the proximity of the empirical (actual) distribution to the theoretical normal distribution. Normal distribution (Gauss-Laplace law) and its characteristics. "Three Sigma Rule". Goodness-of-fit criteria (on the example of the Pearson or Kolgomogorov test).

You can notice a certain relationship in the change in the frequencies and values ​​of the varying attribute. As the value of the attribute grows, the frequencies first increase, and then, after reaching a certain maximum value, they decrease. Such regular changes in frequencies in variational series are called distribution patterns.

To reveal the regularity of the distribution, it is necessary that the variation series contains a sufficiently large number of units, and the series themselves are qualitatively homogeneous aggregates.

The distribution polygon built according to the actual data is empirical (actual) distribution curve, which reflects not only objective (general), but also subjective (random) distribution conditions that are not characteristic of the phenomenon under study.

In practical work, the distribution law is found by comparing the empirical distribution with one of the theoretical ones and assessing the degree of difference or correspondence between them. Theoretical distribution curve reflects in its pure form, without taking into account the influence of random factors, the general pattern of frequency distribution (distribution density) depending on the values ​​of varying features.

In statistics, various types of theoretical distributions are common: normal, binomial, Poisson, etc. Each of the theoretical distributions has its own specifics and scope.

Normal distribution law is characteristic of the distribution of equally probable events occurring during the interaction of many random factors. The law of normal distribution underlies statistical methods for estimating distribution parameters, the representativeness of sample observations, and measuring the relationship of mass phenomena. To check how the actual distribution corresponds to the normal distribution, it is necessary to compare the frequencies of the actual distribution with the theoretical frequencies characteristic of the normal distribution law. These frequencies are a function of normalized deviations. Therefore, according to the empirical distribution series, normalized deviations t are calculated. The theoretical frequencies corresponding to them are then determined. Thus, the empirical distribution is leveled.

Normal distribution or the Gauss-Laplace law is described by the equation
, where y t is the ordinate of the normal distribution curve, or the frequency (probability) of the x value of the normal distribution; – mathematical expectation (average value) of individual x values. If the values ​​(x - ) measure (express) in terms of standard deviation , i.e. in standardized (normalized) deviations t = (x - )/, then the formula will take the form:
. The normal distribution of socio-economic phenomena in its pure form is rare, however, if the homogeneity of the population is observed, often the actual distributions are close to normal. The distribution pattern of the studied quantities is revealed by checking the correspondence of the empirical distribution to the theoretically normal distribution law. To do this, the actual distribution is aligned with the normal curve and calculated consent criteria .

The normal distribution is characterized by two essential parameters that determine the center of grouping of individual values ​​and the shape of the curve: the arithmetic mean and standard deviation . Normal distribution curves differ in the position on the x-axis of the center of distribution and spread around this center  (Fig. 4.1 and 4.2). A feature of the normal distribution curve is its symmetry about the center of distribution - on both sides of its middle, two uniformly decreasing branches are formed, asymptotically approaching the abscissa axis. Therefore, with a normal distribution, the mean, mode and median are the same: = Mo = Me.

  x

The normal distribution curve has two inflection points (transition from convexity to concavity) at t = 1, i.e. when the options deviate from the average (x - ) equal to the standard deviation . Within  with a normal distribution is 68.3%, within 2 – 95.4%, within 3 - 99.7% of the number of observations or frequencies of the distribution series. In practice, there are almost no deviations exceeding 3therefore, the above ratio is called " three sigma rule ».

To calculate the theoretical frequencies, the formula is used:

.

Value
there is a function of t or the density of the normal distribution, which is determined from a special table, excerpts from which are given in Table. 4.2.

Normal distribution density values ​​Table 4.2

The graph in fig. 4.3 clearly demonstrates the closeness of the empirical (2) and normal (1) distributions.

Rice. 4.3. Distribution of postal branches by number

workers: 1 - normal; 2 - empirical

To mathematically substantiate the proximity of the empirical distribution to the normal distribution law, we calculate consent criteria .

Kolmogorov's criterion - a goodness-of-fit criterion that allows one to estimate the degree of closeness of the empirical distribution to the normal one. A. N. Kolmogorov proposed to use the maximum difference between the accumulated frequencies or frequencies of these series to determine the correspondence between the empirical and theoretical normal distributions. To test the hypothesis that the empirical distribution corresponds to the normal distribution law, the goodness of fit criterion is calculated = D/
, where D is the maximum difference between the cumulative (cumulative) empirical and theoretical frequencies, n is the number of population units. According to a special table, P () is determined - the probability of achieving , which means that if the variational attribute is distributed according to the normal law, then from - for random reasons, the maximum discrepancy between the empirical and theoretical accumulated frequencies will be no less than the actually observed one. Based on the value of P(), certain conclusions are drawn: if the probability of P() is large enough, then the hypothesis that the actual distribution corresponds to the normal law can be considered confirmed; if the probability P() is small, then the null hypothesis is rejected, the discrepancies between the actual and theoretical distributions are recognized as significant.

Probability values ​​for goodness of fit  Table 4.3

Pearson criteria 2 ("chi-square") - goodness-of-fit criterion, which allows assessing the degree of closeness of the empirical distribution to the normal one:
, where f i , f" i are the frequencies of the empirical and theoretical distributions in a certain interval. The greater the difference between the observed and theoretical frequencies, the greater the criterion  2. samples, the calculated value of the criterion  2 calc is compared with the tabular  2 calc with the corresponding number of degrees of freedom and a given level of significance. h–l, where h– number of groups; l is the number of conditions that must be satisfied when calculating the theoretical frequencies. To calculate the theoretical frequencies of the normal distribution curve using the formula
you need to know three parameters , , f, so the number of degrees of freedom is h–3. If  2 calc > 2 tab, i.e.  2 falls into the critical region, then the discrepancy between the empirical and theoretical frequencies is significant and cannot be explained by random fluctuations in the sample data. In this case, the null hypothesis is rejected. If  2 calc  2 tab. If the calculated criterion does not exceed the maximum possible frequency discrepancy that can occur due to chance, then in this case the hypothesis of the correspondence of the distributions is accepted. The Pearson criterion is effective with a significant number of observations (n50), and the frequencies of all intervals should be at least five units (with a smaller number, the intervals are combined), and the number of intervals (groups) should be large (h>5), since the estimate  2 depends on the number of degrees of freedom.

Romanovsky criterion - a goodness-of-fit criterion that allows assessing the degree of closeness of an empirical distribution to a normal distribution. Romanovsky suggested that the proximity of the empirical distribution to the normal distribution curve should be estimated in relation to:

, where h is the number of groups.

If the ratio is greater than 3, then the discrepancy between the frequencies of the empirical and normal distributions cannot be considered random, and the hypothesis of a normal distribution should be rejected. If the ratio is less than or equal to 3, then the hypothesis of a normal data distribution can be accepted.

The asymmetry is calculated by the RMSK function. Its argument is the interval of cells with data, for example, =SCOS(A1:A100) if the data is contained in the interval of cells from A1 to A100.

The kurtosis is calculated by the kurtosis function, whose argument is numeric data, usually specified as an interval of cells, for example: =Kurt (A1:A100).

§2.3. Analysis tool Descriptive statistics

AT excel it is possible to calculate all the point characteristics of the sample at once using the analysis tool Descriptive statistics, which is contained in Analysis package.

Descriptive statistics creates a table of key statistics for the data set. This table will contain the following characteristics: mean, standard error, variance, standard deviation, mode, median, range of interval variation, maximum and minimum values, skewness, kurtosis, population size, sum of all population elements, confidence interval (reliability level). Tool Descriptive statistics significantly simplifies the statistical analysis by eliminating the need to call each function to calculate the statistical characteristics separately.

In order to call descriptive statistics, follows:

1) in the menu Service choose a team Data analysis;

2) in the list Analysis tools dialog box Data analysis choose a tool Descriptive statistics and press OK.

In the window Descriptive statistics necessary:

· in a group Input data in field input interval specify the range of cells containing data;

if the first row in the input range contains a column heading, then in field Labels in the first line must be ticked;

· in a group Output options activate the switch (check the box) Final statistics, if you need a complete list of characteristics;

activate the switch Reliability level and specify the confidence in % if you want to calculate the confidence interval (the default is 95% confidence). Click OK.

As a result, a table will appear with the calculated values ​​of the above statistical characteristics. Immediately, without deselecting this table, run the command Format® Column® AutoFit Width.

Dialog view Descriptive statistics:

Practical tasks

2.1. Calculation of basic point statistics using standard functions excel

The same voltmeter measured 25 times the voltage in the circuit section. As a result of the experiments, the following voltage values ​​in volts were obtained:

32, 32, 35, 37, 35, 38, 32, 33, 34, 37, 32, 32, 35,

34, 32, 34, 35, 39, 34, 38, 36, 30, 37, 28, 30.

Find the mean, sample and corrected variance, standard deviation, range, mode, median. Check the deviation from the normal distribution by calculating the skewness and kurtosis.

To complete this task, complete the following steps.

1. Type the results of the experiment in column A.

2. In cell B1, type "Mean", in B2 - "Sample variance", in B3 - "Standard deviation", in B4 - "Corrected variance", in B5 - "Corrected standard deviation", in B6 - "Maximum", in B7 - "Minimum", in B8 - "Range of variation", in B9 - "Mode", in B10 - "Median", in B11 - "Asymmetry", in B12 - "Kurtosis".

3. Justify the width of this column with Auto-match width.

4. Select cell C1 and click on the button with the "=" sign in the formula bar. By using Function Wizards in category Statistical find the AVERAGE function, then select the range of cells with data and press OK.

5. Select cell C2 and click on the = sign in the formula bar. By using Function Wizards in category Statistical find the VARP function, then select the interval of cells with data and press OK.

6. Do the same yourself to calculate the rest of the characteristics.

7. To calculate the range of variation in cell C8, enter the formula: \u003d C6-C7.

8. Add one line in front of your table, in which type the headings of the corresponding columns: "Name of characteristics" and "Numerical values".

To obtain an approximate idea of ​​the form of distribution of a random variable, a graph of its distribution series (a polygon and a histogram), a function or distribution density is plotted. In the practice of statistical research one has to meet with the very different distributions. Homogeneous populations are characterized, as a rule, by unimodal distributions. Multi-vertex indicates the heterogeneity of the studied population. In this case, it is necessary to regroup the data in order to isolate more homogeneous groups.

Finding out the general nature of the distribution of a random variable involves assessing the degree of its homogeneity, as well as calculating the indicators of asymmetry and kurtosis. In a symmetric distribution, in which the mathematical expectation is equal to the median, i.e. , we can assume that there is no asymmetry. But the more noticeable the asymmetry, the greater the deviation between the characteristics of the distribution center - the mathematical expectation and the median.

The simplest coefficient of asymmetry of the distribution of a random variable can be considered , where is the mathematical expectation, is the median, and is the standard deviation of the random variable.

In the case of right-sided asymmetry, left-sided -. If , it is considered that the asymmetry is low, if - medium, and when - high. A geometric illustration of right-sided and left-sided asymmetry is shown in the figure below. It shows graphs of the density of distributions of the corresponding types of continuous random variables.

Picture. Illustration of right-handed and left-handed asymmetries on graphs of densities of distributions of continuous random variables.

There is another coefficient of asymmetry of the distribution of a random variable. It can be proved that the difference from zero of the central moment of odd order indicates the asymmetry of the distribution of the random variable. In the previous indicator, we used an expression similar to the moment of the first order. But usually in this other coefficient of asymmetry, a central moment of the third order is used , and in order for this coefficient to become dimensionless, it is divided by the cube of the standard deviation. This results in the following asymmetry: . For this coefficient of asymmetry, as well as for the first in the case of right-sided asymmetry , left-sided - .

Kurtosis of a random variable

The kurtosis of the distribution of a random variable characterizes the degree of concentration of its values ​​near the center of distribution: the higher such concentration, the higher and narrower the plot of its distribution density will be. The kurtosis (pointedness) indicator is calculated by the formula: , where is the 4th order central moment, and is the standard deviation raised to the 4th power. Since the powers of the numerator and denominator are the same, kurtosis is a dimensionless quantity. At the same time, it is accepted as a standard for the absence of kurtosis, zero kurtosis, to take the normal distribution. But it can be proved that for a normal distribution . Therefore, in the formula for calculating the kurtosis, the number 3 is subtracted from this fraction.

Thus, for a normal distribution, the kurtosis is zero: . If the kurtosis is greater than zero, i.e. , then the distribution is more peaked than normal. If the kurtosis is less than zero, i.e. , then the distribution is less peaked than normal. The limiting value of the negative kurtosis is the value ; the value of positive kurtosis can be infinitely large. How the graphs of peaked and flat-topped densities of the distribution of random variables look in comparison with the normal distribution is shown in the figure.

Picture. Illustration of peaked and flat-topped densities of distribution of random variables in comparison with the normal distribution.

The asymmetry and kurtosis of the distribution of a random variable show how much it deviates from the normal law. For large asymmetries and excesses, the calculation formulas for the normal distribution should not be used. What is the level of admissibility of skewness and kurtosis for the use of normal distribution formulas in the analysis of data of a particular random variable should be determined by the researcher based on his knowledge and experience.

2.6 Skewness and kurtosis

In mathematical statistics, to determine the geometric form of the probability density of a random variable, two numerical characteristics associated with the central moments of the third and fourth orders are used.

Definition 2.22 Sample skewnessx 1 , x 2 , …, x n called the number equal to the ratio of the central sampling moment of the third order to the cube of the standard deviation S:

Since and , then the asymmetry coefficient is expressed in terms of central moments by the following formula:

This yields a formula expressing the asymmetry coefficient in terms of the initial moments:

, which facilitates practical calculations.

The corresponding theoretical characteristic is introduced with the help of theoretical moments.

Definition 2.23 Skewness coefficient of a random variableXcalled a numberequal to the ratio of the central moment of the third orderto the cube of the standard deviation:

If the random variable X has a symmetrical distribution with respect to the mathematical expectation μ, then its theoretical skewness is 0, but if the probability distribution is asymmetric, then the skewness is nonzero. A positive value of the asymmetry coefficient indicates that most of the values ​​of the random variable are located to the right of the mathematical expectation, that is, the right branch of the probability density curve is longer than the left one. A negative value for the skewness indicates that the longer part of the curve is on the left. This statement is illustrated by the following figure.

Figure 2.1 - Positive and negative asymmetry

distributions

Example 2.29 Let's find the sample coefficient of asymmetry according to the study of stressful situations from example 2.28.

Using the previously calculated values ​​of the central sample moments, we obtain

.

Round = 0.07. The non-zero value of the skewness coefficient found shows that the distribution is skewed relative to the mean. A positive value indicates that the longer branch of the probability density curve is on the right.

The features of the distribution of values ​​of a random variable around its modal value X mod are characterized by the following constant.

Definition 2.24 Sampling kurtosisx 1 , x 2 , …, x ncalled a number , equal

,

whereis the selective central moment of the fourth order,

S 4 - the fourth degree of the standarddeviationsS.

The theoretical concept of kurtosis is analogous to sampling.

Definition 2.25 Kurtosis of a random variableXcalled a number e, equal

,

where– theoretical central moment of the fourth order,

–fourth power standard deviation.

The value of kurtosis e characterizes the relative steepness of the top of the distribution density curve around the maximum point. If the kurtosis is a positive number, then the corresponding distribution curve has a sharper peak. A distribution with negative kurtosis has a smoother and flatter top. The following figure illustrates the possible cases.

Figure 2.2 - Distributions with positive, zero and negative kurtosis values