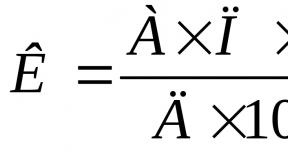A number of results inherent in this action can be noted. These results are called properties of addition of natural numbers. In this article, we will analyze in detail the properties of the addition of natural numbers, write them using letters and give explanatory examples.

Page navigation.

Associative property of addition of natural numbers.

Now we give an example illustrating the associative property of addition of natural numbers.

Imagine a situation: 1 apple fell from the first apple tree, and 2 apples and 4 more apples fell from the second apple tree. Now consider the following situation: 1 apple and 2 more apples fell from the first apple tree, and 4 apples fell from the second apple tree. It is clear that the same number of apples will be on the ground in both the first and second cases (which can be verified by recalculation). That is, the result of adding the number 1 to the sum of the numbers 2 and 4 is equal to the result of adding the sum of the numbers 1 and 2 to the number 4.

The considered example allows us to formulate the associative property of the addition of natural numbers: in order to add a given sum of two numbers to a given number, you can add the first term of this sum to this number and add the second term of this sum to the result obtained. This property can be written using letters like this: a+(b+c)=(a+b)+c, where a , b and c are arbitrary natural numbers.

Please note that in the equality a+(b+c)=(a+b)+c there are parentheses "(" and ")". Parentheses are used in expressions to indicate the order in which actions are performed - actions in brackets are performed first (more on this in the section). In other words, brackets enclose expressions whose values ​​are evaluated first.

In conclusion of this paragraph, we note that the associative property of addition allows us to uniquely determine the addition of three, four and more natural numbers.

The property of adding zero and a natural number, the property of adding zero to zero.

We know that zero is NOT a natural number. So why did we decide to consider the addition property of zero and a natural number in this article? There are three reasons for this. First: this property is used when adding natural numbers in a column. Second: this property is used when subtracting natural numbers. Third: if we assume that zero means the absence of something, then the meaning of adding zero and a natural number coincides with the meaning of adding two natural numbers.

Let us carry out the reasoning that will help us formulate the addition property of zero and a natural number. Imagine that there are no items in the box (in other words, there are 0 items in the box), and a items are placed in it, where a is any natural number. That is, added 0 and a items. It is clear that after this action there are a items in the box. Therefore, the equality 0+a=a is true.

Similarly, if a box contains a items and 0 items are added to it (that is, no items are added), then after this action, a items will be in the box. So a+0=a .

Now we can state the property of addition of zero and a natural number: the sum of two numbers, one of which is zero, is equal to the second number. Mathematically, this property can be written as the following equality: 0+a=a or a+0=a, where a is an arbitrary natural number.

Separately, we pay attention to the fact that when adding a natural number and zero, the commutative property of addition remains true, that is, a+0=0+a .

Finally, we formulate the zero-zero addition property (it is quite obvious and does not need additional comments): the sum of two numbers that are each zero is zero. That is, 0+0=0 .

Now it's time to figure out how the addition of natural numbers is performed.

Bibliography.

• Maths. Any textbooks for grades 1, 2, 3, 4 of educational institutions.
• Maths. Any textbooks for 5 classes of educational institutions.

Topic."Associative property of addition. Parentheses".

Goals. Introduce the associative property of addition, with a new mathematical sign - brackets; improve oral and written computational skills in tabular addition and subtraction of single digits within 20 with the transition through the category.

Educational material. Textbook “Mathematics. Grade 2 "(author N.B. Istomina); notebooks on a printed basis: "Notebook in mathematics 1", "Learning to solve combinatorial problems"; individual cards on maple leaves; 15 expression strips for group work; game "Unravel the ball"; support schemes; individual screens for writing.

DURING THE CLASSES

I. Organizational moment

Teacher. Raise your hands, those of you who love to travel. Today we will go on a mathematical journey through the autumn forest, which is full of mysteries and wonders. And travelers are pioneers. Today you yourself will try to make a discovery. Our motto is: "Take skillfully in every business."

II. Knowledge update

U. Let's go along the forest path so as not to disturb the inhabitants of the forest - only from the side we will watch them.

Game "Unravel the ball"

Equations are written on the board, in which some of the numbers are closed by geometric shapes:

At the teacher's command, the children write down the missing number on individual screens and give an explanation for their actions.

U. Where do we begin to unravel the tangle? Why?

Children. Let's start with the expression 15 - 8, since two numbers are known.

U. Attention! Write on your screens the difference between the numbers 15 and 8.

Children wrote 7 and at the same time they all raised their screens.

- And now what equality do we pay attention to?

D. On the first. There, in addition to the number 12, the same triangle is depicted, which means that there should be a number 7.

U. Right. Reduce 12 by 7.

The children wrote the number 5 on the screens.

D. Let's look at the fourth equality, since there, in addition to the number 9, the same square is depicted as in the first equality. So the number 5 should be written on it.

U. Right. Find the value of the sum of the numbers 5 and 9.

The children wrote the number 14 on the screens.

D. Let's take the second equality, since there, in addition to the number 8, there is the same circle as in the fourth equality. So the number 14 should be written on it.

U. Right. Find the difference between 14 and 8.

Children wrote the number 6 on the screens.

D. Let's take the fifth equality, since there, in addition to the number 40, there is the same rectangle as in the second equality. So the number 6 should be written on it.

U. Right. Find the difference between the numbers 40 and 6.

The children wrote the number 34 on the screens.

III. Introduction to new material

U. The forest path led us to a clearing. Let's look around. Around the trees is a carpet of colorful leaves. Each of you has maple leaves with a task on the table. Two students will work on assignments on the back of the board.

Guess by what rule the equalities on the left and right are written, and insert the numbers into the "windows".

Students complete the task on their own.

- Let's see how the guys who worked at the blackboard completed the task. What can you say about the content of the assignments?

D. All assignments are the same.

U. And how did they fulfill them?

D. Differently.

U. Why did it happen?

D. Not everyone has figured out the rule: one knows more and the other less. This is the first time we have done this task.

IV. Formulation of the topic of the lesson

U. Let's analyze the equalities and find out who completed the task correctly. Let's compare the left parts of the equalities of the first and second columns.

D. They are identical. Add up three numbers.

U. Let's compare the right parts of the equalities of the first and second columns.

D.

- In the second column, the second and third numbers were first added up and the result was added to the first number.

U. What numbers will we insert into the "windows"?

D. 8 + 2 + 5 = 10 + 5
9 + 1 + 7 = 10 + 7
8 + 2 + 5 = 8 + 7
9 + 1 + 7 = 9 + 8

U. Who guessed and can formulate the topic of the lesson?

D. We will add three numbers in different ways.

U. We will get acquainted with one more property of addition. Repeat how three numbers were added?

D. In the first column, the first two numbers were first added, and then the third was added.

- In the second column, the second and third numbers were first added, and the result was added to the first number.

U. How can all this be written down? Perhaps there must be some kind of sign?

D. These are brackets.

U. What do the brackets show?

D. Which action should be taken first.

A note opens on the board.

U. What else have you noticed?

D. Three numbers were added differently, but the value of the sum is the same. It does not depend on the order in which the actions are performed.

U. Let's check if you are right. Open your textbook on p. 47, read the rule. You have now discovered the associative property of addition.

V. Physical education

VI. Primary fixation of the material

U. Read task 127 on p. 48.

D. " Show with brackets which two terms you will replace by the value of the sum, and find the value of each expression.

U. Explain why in some expressions the sum of the first and second numbers was first found and the third was added, while in others the sum of the second and third numbers was added to the first number. Raise your hand if you would like to complete this task yourself. You will work on options. The first column is for students of the 1st option, the second column is for the 2nd option, and the third column is an additional one for those who quickly complete the task.

Two students write on the blackboard. The children are doing the task. All examples are checked.

- Read the expression, the meaning of which is "a round number."

D. 30 + (4 + 6) = 40
60 + (24 + 6) = 90
40 + (37 + 3) = 80

U. Read the expression whose value is 7 less than the largest two-digit number.

D.(20 + 70) + 2 = 92

U. Read an expression whose value is a number consisting of the same number of tens and ones.

D.(30 + 40) + 7 = 77

U. Read an expression whose value is the number before 50.

D. 40 + (6 + 3) = 49

U. The most attentive ones will name expressions whose values ​​we have not yet checked. Explain why in some expressions we first found the sum of the first and second numbers and added the third, while in others we added the sum of the second and third numbers to the first number.

D. It is more convenient for us to add numbers, the addition of which produces a “round” number, so it is faster to make calculations.

U. To memorize a new addition property and quickly recall it if you forgot, you need to choose a scheme consisting of letters or signs. These diagrams are on the classroom walls. Look at them, choose one and explain your choice.

D. All diagrams are correct. In mathematics, Latin letters are used, so we choose a scheme ( a + in) +With = a + (in + With).

VII. Independent work in groups

Students are divided into groups, receive tasks on strips of different colors. It is necessary to find and write down the values ​​of these expressions using the associative property of addition, then attach a strip with the expression on a magnetic board under the corresponding formula:

U. All well done! We continue along the forest path. Guess the riddle about the forest animal:

Not a bird, but flies from tree to tree.

D. This is a squirrel.

U. Right. Help the squirrel stock up for the winter in three hollows. We work in notebooks on a printed basis “Learning to solve combinatorial problems”. We carry out task 20 on p. 20 on their own.

Examination:

Read task 21 on p. twenty.

D. " Arrange the letters about , n , With cells differently.

U. Complete this task on your own.

Children group letters.

– What did you get?

D. There were six options.

U. Circle the options where you get words that make sense.

D. it dream and nose.

U. Name the animals that hibernate for the winter.

D. Bear, hedgehog, already.

U. What winter bird is called the "forest doctor"?

D. Woodpecker. With his beak, he gets insects from under the bark of trees, thereby saving them from pests.

VIII. Lesson summary

U. Our journey through the autumn forest has come to an end. What discovery did you make in class today?

D. To add a third number to the sum of two numbers, you can add the sum of the second and third numbers to the first number. This is the associative property of addition.

U. Who liked the trip, applaud.

Children applaud.

IX. Homework

In "Notebook on Mathematics 1" - p. 33, no. 81.

The article was published with the support of the Eurocontract company, one of the main manufacturers of foam blocks, wall blocks, paving slabs, tongue-and-groove slabs, curbstones and other modern building materials. Currently, one of the first places in popularity among building materials is firmly entrenched in foam concrete. And, I must say, well deserved. In a number of countries, foam concrete blocks are even called "bioblocks", since they consist only of natural components and are an environmentally friendly building material that is safe for humans and the environment. In addition, compared to ordinary concrete, foam concrete weighs much less, and, therefore, it is much easier to transport, and the large size and regular shape of foam concrete blocks greatly simplify their laying. Information about the mass of other advantages of foam concrete blocks and their price can be found in detail on the website evrocontract.ru.

Adding one number to another is pretty easy. Consider an example, 4+3=7. This expression means that three units were added to four units, and as a result, seven units were obtained.
The numbers 3 and 4 that we added together is called terms. And the result of adding the number 7 is called sum.

Sum is the addition of numbers. Plus sign “+”.
In literal form, this example would look like this:

a+b=c

Addition components:
a- term, b- terms, c- sum.
If we add 4 units to 3 units, then as a result of addition we will get the same result, it will be equal to 7.

From this example, we conclude that no matter how we swap the terms, the answer remains unchanged:

This property of terms is called commutative law of addition.

Commutative law of addition.

The sum does not change from changing the places of the terms.

In literal notation, the commutative law looks like this:

a+b=b+a

If we consider three terms, for example, take the numbers 1, 2 and 4. And we perform the addition in this order, first we add 1 + 2, and then we add to the resulting sum of 4, we get the expression:

(1+2)+4=7

We can do the opposite, first add 2 + 4, and then add 1 to the resulting amount. Our example will look like this:

1+(2+4)=7

The answer remains the same. For both types of addition of the same example, the answer is the same. We conclude:

(1+2)+4=1+(2+4)

This addition property is called associative law of addition.

The commutative and associative law of addition works for all non-negative numbers.

Associative law of addition.

To add a third number to the sum of two numbers, you can add the sum of the second and third numbers to the first number.

(a+b)+c=a+(b+c)

The associative law works for any number of terms. We use this law when we need to add numbers in a convenient order. For example, let's add three numbers 12, 6, 8 and 4. It would be more convenient to first add 12 and 8, and then add the sum of two numbers 6 and 4 to the resulting sum.
(12+8)+(6+4)=30

Addition property with zero.

When you add a number to zero, the result is the same number.

3+0=3
0+3=3
3+0=0+3

In a literal expression, addition with zero would look like this:

a+0=a
0+ a=a

Questions about the addition of natural numbers:
Addition table, compile and see how the property of the commutative law works?
An addition table from 1 to 10 might look like this:

The second version of the addition table.

If we look at the addition tables, we can see how the commutative law works.

In the expression a + b \u003d c, what will be the sum?
Answer: The sum is the sum of the terms. a+b and c.

In the expression a + b \u003d c terms, what will be?
Answer: a and b. The terms are the numbers that we add.

What happens to a number if you add 0 to it?
Answer: nothing, the number will not change. When added to zero, the number stays the same because zero is the absence of ones.

How many terms must be in the example so that the associative law of addition can be applied?
Answer: from three terms and more.

Write down the commutative law in literal terms?
Answer: a+b=b+a

Examples for tasks.
Example #1:
Write down the answer for the presented expressions: a) 15+7 b) 7+15
Answer: a) 22 b) 22

Example #2:
Apply the combination law to the terms: 1+3+5+2+9
1+3+5+2+9=(1+9)+(5+2)+3=10+7+3=10+(7+3)=10+10=20
Answer: 20.

Example #3:
Solve the expression:
a) 5921+0 b) 0+5921
Solution:
a) 5921+0 =5921
b) 0+5921=5921

Adding one number to another is pretty easy. Consider an example, 6+3=9. This expression means that three units were added to six units, and as a result, nine units were obtained. Or, if we consider the numerical segment: first we moved along it by 6 units, and then by 3, and ended up at point 9. The numbers 6 and 3 that we added are called terms. And the result of addition - the number 9 - is called the sum. In the form of a literal expression, this example will look like this: a + b \u003d c, where a is the term, b is the terms, c is the sum.
If we add 6 units to 3 units, then as a result of addition we will get the same result, it will be equal to 9. From this example, we conclude that no matter how we swap the terms, the answer remains unchanged: 6+3=3+6= 9

This property of terms is called the commutative law of addition.

Commutative (communicative) law of addition:
a + b = b + a.

The sum does not change from changing the places of the terms.

55 + 21 = 21 + 55 = 76
108 + 2 = 2 + 108 = 110

If we consider three terms, for example, take the numbers 1, 2 and 6 and perform the addition in this order, first add 1 + 2, and then add 6 to the resulting sum, then we get the expression: (1 + 2) + 6 \u003d 9
We can do the opposite, first add 2+6, and then add 1 to the resulting amount. Our example will look like this: 1+(2+6)=9
The answer remains the same. For both types of addition of the same example, the answer is the same. We conclude: (1+2)+6=1+(2+6)

This property of addition is called the associative law of addition.

Associative (associative) law of addition:
a + b + c = a + (b + c).

The sum does not change if any group of adjacent terms is replaced by their sum.

197 + 23 + 77 = 197 + (23 + 77) = 197 + 100 = 297.

Note from 7 gurus: both laws are valid for any number of terms. The commutative and associative laws of addition work for all non-negative numbers.

The commutative and associative properties are used for convenience and simplification of calculations during addition.

Need to find the sum 23 + 9 + 7
Using the commutative law, we swap the terms 9 and 7, we get 23 + 7 + 9,
now, using the combination property, we combine 23 and 7, since they give a round number: (23 + 7) + 9,
First add 23 and 7, their sum is 30.
Then we add nine: 30 + 9 = 39.
So: 23 + 9 + 7 = (23 + 7) + 9 = 36

Addition property with zero.

Adding zero to a number does not change that number: a + 0 = 0 + a = 0.

Addition has two properties: commutative and associative.

Commutative property of addition

If the terms are interchanged, the sum will not change. Indeed, when the terms are rearranged, the number of units contained in each of them will not change, and, consequently, the number of units contained in the sum will not change either. This can be easily verified by considering the following example.

Let's calculate the sum of two numbers 3 and 4 in two ways. We can first take the number 3 and add the number 4 to it, resulting in the number 7:

Or take the number 4 first and add the number 3 to it, the total will again be the number 7:

Thus, between the expressions 3 + 4 and 4 + 3, you can put an equal sign, since they are equal to the same value:

commutative property of addition:

Rearranging the terms does not change the sum.

commutative law of addition.

In general, using letters, the commutative property of addition can be written as follows:

a + b = b + a

where a and b

Associative property of addition

The result of adding three or more numbers does not depend on the sequence of actions. This means that the terms can be grouped in any way for the convenience of calculations. This can be easily verified by considering the following example.

We calculate the sum of the three terms 1, 3 and 4 in two ways:

To calculate the value of an expression, we can first add the numbers 1 and 3 and add the number 4 to the result. For clarity, the sum of the numbers 1 and 3 can be enclosed in brackets to indicate that this sum will be calculated first:

1 + 3 + 4 = (1 + 3) + 4 = 4 + 4 = 8

Or first add the numbers 3 and 4 and add the result to the number 1:

1 + 3 + 4 = 1 + (3 + 4) = 1 + 7 = 8

Thus, between the expressions (1 + 3) + 4 and 1 + (3 + 4) you can put an equal sign, since they are equal to the same value:

(1 + 3) + 4 = 1 + (3 + 4)

The same will happen if any other natural numbers are taken as terms.

The considered example allows us to formulate associative property of addition:

The sum of three or more terms does not depend on the sequence of actions.

This property is also called associative law of addition.

In general, using letters, the associative property of addition can be written as follows:

a + (b + c) = (a + b) + c

where a, b and c are arbitrary natural numbers.