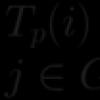alustades ja jätkates mainitud k klemmidega.

Grammatikat nimetatakse LL(k)-grammatikaks, kui see on mõne k puhul LL(k)-grammatika.

Näide 4.7. Kaaluge grammatikat G = ((S, A, B), (0, 1, a, b), P, S), kus P koosneb reeglitest

S -> A | B, A -> aAb | 0, B -> aBbb | üks.

siin . G ei ole ühegi k jaoks LL(k)-grammatika. Intuitiivselt, kui me alustame piisavalt pika märgijada a lugemisega, siis me ei tea, kumba reeglitest S -> A ja S -> B esimesena rakendati, kuni näeme 0 või 1 .

Pöördudes LL (k)-grammatika täpse definitsiooni poole, seame ja y = a k 1b 2k . Siis järeldused

vastavad määratluse järeldustele (1) ja (2). Stringide x ja y esimesed k tähemärki sobivad. Järeldus on aga vale. Kuna k valitakse siin suvaliselt, ei ole G LL-grammatika.

LL(k)-grammatika definitsiooni tagajärjed

Teoreem 4.6. CS grammatika on LL(k)-grammatika siis ja ainult siis, kui kahe erineva reegli jaoks ja R ristmikult tühi kõigi selliste jaoks , mida .

Tõestus. Vaja. Oletame, et ja täidavad teoreemi tingimused ning sisaldab x . Seejärel on FIRST definitsiooni kohaselt mõne y ja z jaoks järeldused

(Pange tähele, et siin oleme kasutanud tõsiasja, et N ei sisalda kasutuid mitteterminale, nagu eeldatakse kõigi vaadeldavate grammatikate puhul.) Kui |x|< k ; то y = z = e . Так как , то G не LL (k)- грамматика .

Adekvaatsus. Oletame, et G ei ole LL(k)-grammatika.

Siis on kaks järeldust

et stringid x ja y langevad kokku esimeses k positsioonis, kuid . Seetõttu ja erinevad reeglid P-st ja igast komplektist ja sisaldab stringi FIRST k (x), mis sobib stringiga FIRST k (y) .

Näide 4.8. Grammatika G, mis koosneb kahest reeglist S -> aS | a , ei ole LL(1)-grammatika, kuna

ESIMESE 1 (aS) = ESIMESE 1 (a) = a.

Intuitiivselt saab seda seletada järgmiselt: tähemärgiga a algava stringi parsimisel näeme ainult seda esimest märki, me ei tea, kumba reeglitest S -> aS või S -> a peaks rakendama S . Teisest küljest on G LL(2)-grammatika. Tõepoolest, äsja esitatud teoreemi tähistuses, kui , siis A = S ja . Kuna S jaoks on antud ainult kaks täpsustatud reeglit, siis ja . Kuna FIRST2(aS) = aa ja FIRST2(a) = a , siis viimase teoreemi järgi on G LL (2)-grammatika.

Vasakpoolse rekursiooni eemaldamine

Peamine raskus ennustava analüüsi kasutamisel on sisestuskeele grammatika leidmine, mida saab kasutada üheselt määratletud sisenditega analüüsitabeli koostamiseks. Mõnikord saab mõne lihtsa teisendusega mitte-LL(1) grammatika taandada samaväärseks LL(1) grammatikaks. Nendest teisendustest on kõige tõhusamad vasakpoolne faktoriseerimine ja vasakpoolse rekursiooni eemaldamine. Siin tuleb teha kaks märkust. Esiteks ei muutu iga grammatika pärast neid teisendusi LL(1)-ks ja teiseks võib pärast selliseid teisendusi tekkiv grammatika muutuda vähem arusaadavaks.

Vahetu vasakpoolse rekursiooni, st vormi rekursiooni saab eemaldada järgmisel viisil. Esiteks rühmitame A-reeglid:

kus ükski rida ei alga tähega A . Seejärel asendame selle reeglistiku järgmisega

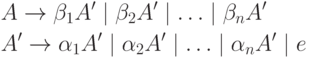
kus A" on uus mitteterminal. Samad ahelad saab tuletada ka mitteterminaalsest A-st, kuid nüüd pole vasakpoolset rekursiooni. See protseduur eemaldab kõik vahetud vasakpoolsed rekursioonid, kuid ei eemalda vasakpoolset rekursiooni, mis hõlmab kahte või enamat samme. Allpool algoritm 4.8 võimaldab eemaldada grammatikast kõik vasakpoolsed rekursioonid.

Algoritm 4.8. Vasakpoolse rekursiooni eemaldamine.

sissepääs. COP-grammatika G ilma e-reegliteta (vormil A -> e ).

Välju. COP-grammatika G" ilma vasakpoolse rekursioonita, samaväärne G .

meetod. Järgige samme 1 ja 2.

(1) Järjesta grammatika G mitteterminalid suvalises järjekorras.

(2) Tehke järgmine protseduur:

Pärast (i-1)-ndat välimise tsükli iteratsiooni sammus 2 mis tahes vormireegli jaoks , kus k< i , выполняется s >k . Selle tulemusena suurendab sisemine tsükkel (j võrra) järgmisel iteratsioonil (j võrra) mis tahes reegli alumist piiri m võrra kuni m >= i . Seejärel pärast A i -reeglite vahetu vasakpoolse rekursiooni eemaldamist muutub m suuremaks kui i .

Ülalt-alla rekursiivse sõelumise korral võib tekkida lõpmatu tsükli probleem.

Aritmeetiliste toimingute grammatikas põhjustab teise reegli rakendamine parsimisprotseduuri tsükli. Selliseid grammatikaid nimetatakse vasakpoolseteks rekursiivseteks. Grammatikat nimetatakse vasakpoolseks rekursiivseks, kui see sisaldab mitteterminali A, mille kohta on tuletis A=>+Aa. Lihtsatel juhtudel nimetatakse vasakpoolset rekursiooni vormireeglite järgi

Sel juhul võetakse kasutusele uus mitteterminal ja algsed reeglid asendatakse järgmistega.

(kui on olemas mitteterminal A, mille jaoks on 1 või enama sammuga väljund A→+Aa). Vasakpoolset rekursiooni saab vältida grammatika teisendamisega.

Näiteks lavastused A→Aa

Võib asendada samaväärsega:

Sellisel juhul on olemas algoritm, mis välistab vasakpoolse rekursiooni:

1) määrake mitteterminalide hulgal mingi järjekord (А 1 , А 2 , …, А n)

2) võtame iga mitteterminali, kui selle jaoks on produktsioon, mis arvestab mitteterminali vasakule, ja teisendame grammatika:

i:=1 kuni n teha

j:=1 kuni i-1 puhul teha

kui Ai → Ajγ, siis Ai→δ1γ

│ δkγ, kus

Aj → δ1│ δ2│ …│ δk

3) välistada kõik otsese vasakpoolse rekursiooni juhud (reegel 1)

See. Algoritm aitab vältida silmust.

Vasakpoolse rekursiooni kõrvaldamine aritmeetiliste avaldiste grammatikast ja vasakpoolse rekursiooni välistamise reegli üldvorm:

Vasakpoolse rekursiooni välistamise reegli üldvaade

Vasakpoolne faktoriseerimine.

LL(1) grammatika on vajalik selleks, et valida õige produktsioon ülevalt alla sõelumiseks, et ei tekiks silmust.

Mõnikord on võimalik vasakpoolset faktoriseerimise meetodit kasutades grammatika teisendada LL(1) vormiks.

Näiteks: S → kui B, siis S

│kui B, siis S muidu S

Need produktsioonid rikuvad LL(1)-grammatika tingimust. Selle grammatika saab teisendada kujule LL(1).

S → kui B siis S Saba

V üldine vaade seda teisendust saab määratleda järgmiselt:

võtame kasutusele uue mitteterminali B, mille jaoks

| β N Vasakpoolset faktoriseerimist saab rakendada B-le. Seda protseduuri korratakse seni, kuni toodete valik jääb ebakindlaks (st kuni selles saab midagi muuta).

ESIMESE komplekti ehitamine

Mitteterminali esimene komplekt määratleb terminalide komplekti, millega see mitteterminal võib alata.

1. Kui x on terminal, siis esimene(x)=(x). Kuna ühest terminalist pärineva jada esimene märk saab olla ainult terminal ise.

2. Kui grammatika sisaldab reeglit Хà e, siis hulka first(х) kuulub e. See tähendab, et X võib alata tühja jadaga, st seda ei saa üldse eksisteerida.

3. Kõigi vormiga XàY1 Y2 … Yk lavastuste puhul teeme järgmist. Lisame hulka esimene(X) hulga esimene(Yi), kuni esimene(Yi-1) sisaldab e ja esimene(Yi) ei sisalda e. Sel juhul muutub i 0-st k-ks. See on vajalik, kuna kui Yi-1 võib puududa, siis on vaja välja selgitada, kust kogu jada sel juhul algab.

Vasakpoolset rekursiooni sisaldav grammatika ei ole LL(1) grammatika. Kaaluge reegleid

A→ aa(vasak rekursioon A-s)

A→ a

Siin a eelkäija märk mõlema mitteterminaalse variandi jaoks A. Samamoodi ei saa vasakpoolset rekursiivset tsüklit sisaldav grammatika olla näiteks LL(1) grammatika

A→ eKr

B→ CD

C→ AE

Vasakpoolset rekursiivset tsüklit sisaldava grammatika saab teisendada grammatikaks, mis sisaldab ainult otsest vasakpoolset rekursiooni, ja lisaks täiendavate mitteterminalide kasutuselevõtuga saab vasakpoolse rekursiooni täielikult välistada (tegelikult asendatakse see parempoolse rekursiooniga, mis ei ole probleem LL(1) -omaduste puhul).

Vaatleme näiteks generatiivsete reeglitega grammatikat

S→ aa

A→ bb

B→ CC

C→ Dd

C→ e

D→ Az

millel on vasakpoolne rekursiivne tsükkel, mis hõlmab A, B, C, D. Selle silmuse asendamiseks otsese vasakpoolse rekursiooniga järjestame mitteterminalid järgmiselt: S, A, B, C, D.

Võtke arvesse kõiki vormi genereerimisreegleid

Xi→ Xj γ,

kus Xi ja Xj on mitteterminalid ja γ – terminali ja mitteterminali märkide jada. Seoses reeglitega, mille jaoks j ≥ i, midagi ette ei võeta. See ebavõrdsus ei saa aga kehtida kõigi reeglite puhul, kui on olemas vasakpoolne rekursiivne tsükkel. Valitud järjekorras järgime ühte reeglit:

D→ Az

sest A eelneb D selles järjekorras. Nüüd hakkame asendama A, kasutades kõiki kehtivaid reegleid A vasakul pool. Selle tulemusena saame

D→ bbz

Niivõrd kui B eelneb D järjestamisel korratakse protsessi, andes reegli:

D→ ccbz

Seejärel kordub see veel kord ja annab kaks reeglit:

D→ ecbz

D→ Ddcbz

Nüüd näeb teisendatud grammatika välja selline:

S→ aa

A→ bb

B→ CC

C→ Dd

C→ e

D→ Ddcbz

D→ ecbz

Kõigil neil genereerimisreeglitel on nõutav vorm ja vasakpoolne rekursiivne tsükkel asendatakse otsese vasakpoolse rekursiooniga. Otsese vasakpoolse rekursiooni välistamiseks võtame kasutusele uue mitteterminaalse sümboli Z ja muuta reegleid

D→ ecbz

D→ Ddcbz

D→ ecbz

D→ ecbzZ

Z→ dcbz

Z→ dcbzZ

Pange tähele, et enne ja pärast teisendust D genereerib regulaaravaldise

(ecbz) (dcbz)*

Üldistades võib näidata, et kui mitteterminaalne A kuvatakse vasakul küljel r+ s reeglite loomine, r millest kasutatakse otsest vasakpoolset rekursiooni ja s- ei, st.

A→ Aα 1, A→ Aα 2,..., A→ Aα r

A→ β 1, A→ β 2,..., A→ β s

siis saab need reeglid asendada järgmistega:

Mitteametlik tõend on see, et enne ja pärast transformatsiooni A genereerib regulaaravaldise ( β 1 | β 2 |... | β s) ( α 1 | α 2 |... | α r) *

Tuleb märkida, et vasakpoolse rekursiooni (või vasakpoolse rekursiivse tsükli) välistades ei saa me ikkagi LL(1) grammatikat, sest mõne mitteterminali puhul on saadud grammatika reeglite vasakus servas alternatiivsed parempoolsed osad, mis algavad samade tähemärkidega. Seetõttu tuleks pärast vasakpoolse rekursiooni kõrvaldamist jätkata grammatika teisendamist LL(1) vormile.

17. Grammatikate teisendamine LL(1)-vormingusse. Faktoriseerimine.

Faktoriseerimine

Paljudes olukordades saab LL(1) funktsiooni puudumisel grammatika faktoriseerimise protsessi abil teisendada LL(1) grammatikateks. Vaatleme näidet sellisest olukorrast.

P→ alusta D; KOOS lõpp

D→ d, D

D→ d

KOOS→ s; KOOS

KOOS→ s

Faktoriseerimise protsessis asendame mitu reeglit ühe mitteterminali jaoks vasakul pool, mille parem pool algab sama sümboliga (sümbolite jada) ühe reegliga, kus paremal pool ühisele algusele järgneb lisaks kasutusele mitteterminal. Grammatikat täiendatakse ka täiendava mitteterminali reeglitega, mille järgi tuletatakse sellest reegli algse parempoolse külje erinevad “jäänused”. Ülaltoodud grammatika jaoks annaks see järgmise LL(1) grammatika:

P→ alusta D; KOOS lõpp

D→ d X X)

X→ , D(vastavalt 1. reeglile D algne grammatika jaoks d järgib, D)

X→ ε (vastavalt 2. reeglile D algne grammatika jaoks d mitte midagi (tühi string)

KOOS→ s Y(Tutvustame täiendavat mitteterminali Y)

Y→ ; KOOS(vastavalt 1. reeglile C algne grammatika jaoks s järgneb; C)

Y→ ε (vastavalt 2. reeglile C algne grammatika jaoks s mitte midagi (tühi string)

Samamoodi reeglite genereerimine

S→ aSb

S→ aSc

S→ ε

saab teisendada faktoriseerimisega reegliteks

S→ aSX

S→ ε

X→ b

X→ c

ja saadud grammatika on LL(1). Faktoriseerimise protsessi ei saa aga automatiseerida, laiendades seda üldjuhtumile. Järgmine näide näitab, mis võib juhtuda. Kaaluge reegleid

1. P→ Qx

2. P→ Ry

3. K→ sQm

4. K→ q

5. R→ sRn

6. R→ r

Mõlemad juhtmärkide komplektid kahe valiku jaoks P sisaldama s, ja püüdes "vastu pidada s sulgudest välja", asendame K ja R reeglite 1 ja 2 paremates osades:

P→ sQmx

P→ sRny

P→ qx

P→ ry

Need reeglid võib asendada järgmistega:

P→ qx

P→ ry

P→ sp 1

P 1 → Qmx

P 1 → Rny

Reeglid jaoks P1 sarnased algsete reeglitega P ja neil on kattuvad juhtmärkide komplektid. Saame neid reegleid muuta samamoodi nagu reeglid P:

P 1 → sQmmx

P 1 → qmx

P 1 → sRny

P 1 → rny

Faktooring, saame

Formaalsete grammatikate ja automaatide (TFGiA) teoorias on oluline roll nn. kontekstivabad grammatikad(CS-grammatika). CS-grammatika on nelik, mis koosneb mitteterminaalsete sümbolite hulgast N, terminali sümbolite hulgast T, reeglite (produktsioonide) hulgast P ja hulka N kuuluvast algsümbolist S.

Iga P produktsioon p on kujul A –> a, kus A on mitteterminaalne märk (A-st N-st) ja a on string, mis koosneb terminali ja mitteterminaalsetest märkidest. Sõnaväljundprotsess algab stringiga, mis sisaldab ainult algusmärki S. Pärast seda asendatakse igas etapis üks aktiivses stringis sisalduvatest mitteterminaalsetest märkidest ühe produktsiooni parema poolega, milles see on vasak pool. Kui pärast sellist toimingut saadakse string, mis sisaldab ainult terminali märke, siis väljundprotsess lõpeb.

Paljude teoreetiliste probleemide puhul on mugav käsitleda nn normaalsed vormid grammatik Grammatika normaliseerimise protsess algab sageli vasakpoolse rekursiooni kõrvaldamisega. Selles ülesandes käsitleme ainult selle erijuhtu, mida nimetatakse otseseks vasakpoolseks rekursiooniks. Järeldusreegel A -> R sisaldab vahetut vasakpoolset rekursiooni, kui stringi R esimene märk on A.

CS-grammatika on antud. On vaja leida reeglite arv, mis sisaldavad vahetut vasakpoolset rekursiooni.

Sisendandmed

Sisendfaili INPUT.TXT esimene rida sisaldab grammatika reeglite arvu n (1 ≤ n ≤ 1000). Iga järgmine n rida sisaldab ühte reeglit. Mitteterminaalseid sümboleid tähistatakse ingliskeelse tähestiku suurtähtedega, terminali sümbolid - väiketähtedega. Lavastuse vasakpoolne osa on paremast eraldatud sümbolitega –>. Lavastuse parempoolne osa on 1–30 tähemärgi pikkune.