Ex Twee Ma Function. Ascending and descending function on the interval, extremes. Derivative and its role
The function of the extremum function is the point of the function definition area in which the function value takes the minimum or maximum value. The values \u200b\u200bof the function at these points are called extremes (minimum and maximum) functions.
Definition. Point x.1 Function definition areas f.(x.) Called point of maximum function if the value of the function at this point is more functions of the function in fairly close to it points located on the right and to the left of it (that is, inequality is performed f.(x.0 ) > f.(x.0 + Δ x.) x.1 maximum.
Definition. Point x.2 Function definition areas f.(x.) Called point of minimum functionif the value of the function at this point is less than the values \u200b\u200bof the function in fairly close to it points located on the right and to the left of it (that is, inequality is performed f.(x.0 ) < f.(x.0 + Δ x.) ). In this case, it is said that the function has at the point x.2 minimum.
Suppose point x.1 - point maximum function f.(x.). Then in the interval before x.1 the function is increasing , therefore, the derivative function is greater than zero ( f. "(x.)\u003e 0), and in the interval after x.1 Function decreases, therefore, and derived function Less zero ( f. "(x.) < 0 ). Тогда в точке x.1
Suppose also that point x.2 - point minimum function f.(x.). Then in the interval before x.2 The function decreases, and the derivative function is less than zero ( f. "(x.) < 0 ), а в интервале после x.2 The function increases, and the derivative function is greater than zero ( f. "(x.)\u003e 0). In this case, also at the point x.2 The derivative function is zero or does not exist.
Farm Theorem (necessary sign of existence of an extremum function). If point x.0 - Extremum Point Functions f.(x.), then at this point the derivative function is zero ( f. "(x.) \u003d 0) or does not exist.
Definition. Points in which the derivative function is zero or does not exist are called critical points .

Example 1. Consider a function.
At point x. \u003d 0 derivative function equal to zero, therefore, point x. \u003d 0 is a critical point. However, as can be seen on the graph of the function, it increases in the entire field of definition, so the point x. \u003d 0 is not an extremum point of this function.
Thus, the conditions that the derivative of the function at the point is zero or does not exist, are the necessary conditions of extremum, but not sufficient, since other examples of functions can be cited, for which these conditions are performed, but the function does not have an extremum at the appropriate point. therefore need to have sufficient signsAllowing to be judged, there is an extremum at a particular critical point and which is a maximum or a minimum.
Theorem (the first sufficient feature of the existence of an extremum function). Critical point x.0 f.(x.) If during the transition through this point the derivative function changes the sign, and if the sign changes from the "plus" to "minus", then the point of the maximum, and if with a "minus" on the "plus", then the minimum point.
If near the point x.0 , on the left and right of it, the derivative saves a sign, then this means that the function or only decreases, or only increases in some neighborhood of the point x.0 . In this case at the point x.0 Extremum is not.
So, to determine the extremma points of the function, you need to do the following :
- Find a derivative function.
- Equate the zero derivative and determine the critical points.
- Mentally or on paper, note the critical points on the numeric axis and determine the signs of the derived function in the obtained intervals. If the sign of the derivative changes with the "plus" to "minus", the critical point is a maximum point, and if with a "minus" on the "plus", then the minimum point.
- Calculate the value of the function at extremum points.

Example 2. Find Extreme Functions ![]() .
.
Decision. Find a derivative function:
We equate the derivative of zero to find critical points:
![]() .
.
Since for any "IKSA" values, the denominator is not equal to zero, then equalize the numerator:
Got one critical point x. \u003d 3. Determine the sign of the derivative in the intervals delimited by this point:
in the interval from minus infinity up to 3 - a minus sign, that is, the function decreases,
in the range from 3 to plus infinity - a sign plus, that is, the function increases.
That is, point x. \u003d 3 is a minimum point.
Find the function value at the minimum point:
Thus, the extremum point of the function is found: (3; 0), and it is a minimum point.
Theorem (the second sufficient feature of the existence of the extremum function). Critical point x.0 is a point of extremum function f.(x.) if the second derivative function at this point is not zero ( f. ""(x.) ≠ 0), and if the second derivative is greater than zero ( f. ""(x.)\u003e 0), then the maximum point, and if the second derivative is less than zero ( f. ""(x.) < 0 ), то точкой минимума.
Note 1. If at the point x.0 Apply to zero and the first, and the second derivatives, then at this point it is impossible to judge the presence of an extremum on the basis of the second sufficient feature. In this case, you need to take advantage of the first sufficient feature of the extremum function.
Remark 2. The second sufficient feature of the extremum function is not applicable and then when the first derivative does not exist at the stationary point (then there is no second derivative). In this case, you also need to enjoy the first sufficient feature of the extremum function.
Local nature of extremums function
From the given definitions it follows that the extremum of the function has a local character - this is the largest and smallest value of the function compared to the next values.
Suppose you consider your earnings in the length of time with a length of one year. If you have earned 45 000 rubles in May, and in April 42,000 rubles and in June 39,000 rubles, then the May earnings are the maximum of earning functions compared to the next values. But in October you earned 71,000 rubles, in September 75,000 rubles, and in November 74,000 rubles, so the October earnings - minimum of the functions of earnings compared to nearby values. And you can easily see that the maximum among the events of April-May-June less than the minimum of September-October-November.
Speaking generalized, the function may have several extremums on the interval, and it may turn out that any minimum function is more than a maximum. So, for the function shown in the figure above,.
That is, it should not be thought that the maximum and minimum of the functions are, respectively, its greatest and the smallest values \u200b\u200bon the entire segment under consideration. At the maximum point, the function is most important only compared to those values \u200b\u200bthat it has in all points, quite close to the maximum point, and at the point of the minimum - the smallest value only compared to those values \u200b\u200bthat it has in all points, close enough To a minimum point.
Therefore, it is possible to clarify the above concept of extremum points of the function and call the point of minimum to the local minimum points, and the maximum points are the local maximum points.
We are looking for extremum functions together

Example 3.
Decision. Function is defined and continuous on the entire numerical direct. Its derivative ![]() There is also a whole numerical direct. Therefore, in this case, only those in which, i.e. are critical points. , From where. Critical points and split the entire field of determining the function to three monotony intervals :. We choose in each of them at one checkpoint and find a sign of the derivative at this point.
There is also a whole numerical direct. Therefore, in this case, only those in which, i.e. are critical points. , From where. Critical points and split the entire field of determining the function to three monotony intervals :. We choose in each of them at one checkpoint and find a sign of the derivative at this point.
For the interval, the control point can be: we find. Taking a point in the interval, we get, and taking the point in the interval, we have. So, in the intervals and, and in the interval. According to the first sufficient attitude of the extremum, there is no extremum at the point (as the derivative saves a sign in the interval), and at the point the function has a minimum (since the derivative of the transition changes through this point with a minus plus). Find the appropriate values \u200b\u200bof the function: as well. In the interval, the function decreases, because in this interval, and in the interval increases, because in this interval.
To clarify the construction of the graph, find the intersection points with the coordinate axes. When you obtain the equation, the roots of which and, i.e., two points are found (0; 0) and (4; 0) function graphics. Using all the information received, we build a schedule (see at the beginning of the example).
For self-test, when calculated can be used online calculator derivatives .

Example 4.Find extremmas functions and build its schedule.
The field definition area is the entire number direct, except for the point, i.e. .
To reduce the study, you can use the fact that this function is measurable, since  . Therefore, its schedule is symmetrical with respect to the axis Oy. And the study can be performed only for the interval.
. Therefore, its schedule is symmetrical with respect to the axis Oy. And the study can be performed only for the interval.
Find a derivative ![]() and critical points of function:
and critical points of function:
1) 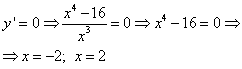 ;
;
2) ![]() ,
,
but the function suffers the gap at this point, so it cannot be an extremum point.
Thus, the specified function has two critical points: and. Considering the readiness of the function, check on the second sufficient sign of extremum only the point. To do this, find the second derivative ![]() And we define her sign when: we get. Since it is a point of a minimum function, while
And we define her sign when: we get. Since it is a point of a minimum function, while ![]() .
.
To make a more complete picture of the function of the function, find out its behavior on the boundaries of the definition area:

(here the symbol is indicated by the desire x. to zero on the right, and x. remains positive; Similarly means the desire x. to zero on the left, and x. It remains negative). Thus, if, then. Next, found
 ,
,
those. If, then.
Points of intersection with the axes of the graph function has no function. Figure - at the beginning of the example.
For self-test, when calculated can be used online calculator derivatives .
We continue to look for extremmas functions together.
Example 8.Find extremmas functions.

Decision. Find the function definition area. Since there should be inequality, then we get.
Find the first derivative function.
In July 2020, NASA launches an expedition to Mars. The spacecraft will deliver an electronic media to Mars with the names of all registered expedition participants.
Registration of participants is open. Get your ticket for Mars on this link.
If this post decided your problem or just liked you, share a link to it with my friends on social networks.
One of these code options must be copied and insert into the code of your webpage, preferably between the tags
and or immediately after the tag . According to the first version, MathJax is loaded faster and slows down the page. But the second option automatically tracks and loads the latest MathJax versions. If you insert the first code, it will need to be periodically updated. If you insert the second code, the pages will be loaded slower, but you will not need to constantly monitor MathJax updates.Connect MathJax is the easiest way to Blogger or WordPress: Add a widget for inserting a third-party JavaScript code to insert the first or second version of the download code presented above and place the widget closer to the beginning of the template (by the way, it is not at all necessary Since the MathJax script is loaded asynchronously). That's all. Now read Mathml, Latex and Asciimathml markup syntax, and you are ready to insert mathematical formulas on the web pages of your site.
Another New Year's Eve ... Frosty Weather and Snowflakes on the window glass ... All this prompted me to again write about ... Fractals, and about what he knows about this Alpha tungshes. On this occasion, there is an interesting article in which there are examples of two-dimensional fractal structures. Here we will consider more complex examples of three-dimensional fractals.
The fractal can be clearly imagined (describe), as a geometric shape or body (having in mind that both there are many, in this case, a set of points), the details of which have the same shape as the original figure itself. That is, it is a self-like structure, considering the details of which with an increase, we will see the same form as without increasing. Whereas in the case of a conventional geometric shape (not fractal), with an increase we will see parts that have a simpler form than the original figure itself. For example, with a sufficiently large increase, the part of the ellipse looks like a straight line. With fractals, this does not happen: with any increases, we will again see the same complex shape, which will repeat again and again.
Benoit Mandelbrot (Benoit Mandelbrot), the founder of the science of fractals, in his article Fractals and art in the name of science wrote: "Fractals are geometric forms that are equally complex in their details, as in its general form. That is, if Part of the fractal will be increased to the size of the whole, it will look like an integer, or exactly, or, possibly, with a small deformation. "
Very important information about the behavior of the function provides gaps of increasing and descending. Their finding is part of the process of researching function and building a schedule. In addition, extremum points in which there is a shift from an increase in decay or decrease to increase, special attention is paid when finding the greatest and smallest function value at some interval.
In this article, we will give the necessary definitions, we formulate a sufficient sign of increasing and descending the function at the interval and sufficient conditions for the existence of extremum, we will apply all this theory to solve examples and tasks.
Navigating page.
Ascending and descending function on the interval.
Definition of an increasing function.
The function y \u003d f (x) increases on the interval x, if for any and ![]() Inequality is performed. In other words, the greater value of the argument corresponds to the greater value of the function.
Inequality is performed. In other words, the greater value of the argument corresponds to the greater value of the function.
Determining a decreasing function.
The function y \u003d f (x) decreases on the interval X, if for any and ![]() Inequality is performed
Inequality is performed ![]() . In other words, the greater value of the argument corresponds to the smaller value of the function.
. In other words, the greater value of the argument corresponds to the smaller value of the function.

Note: If the function is determined and continuous at the ends of the increasing or decrease interval (a; b), that is, with x \u003d a and x \u003d b, these points are included in an increase in increasing or descending. This does not contradict the definitions of the increasing and descending function at the interval x.
For example, we know from the properties of the basic elementary functions that y \u003d sinx is defined and continuous for all valid values \u200b\u200bof the argument. Therefore, from an increase in the function of sinus on the interval we can argue about increasing on the segment.
Extremum points, extremmas function.
Call called maximum point The functions y \u003d f (x), if for all x from its surrounding the inequality. The value of the function at the maximum point is called maximum function And denote.
Call called point of minimum The functions y \u003d f (x), if for all x from its surrounding the inequality. The value of the function at the point of the minimum is called minimum function And denote.
Under the neighborhood points understand the interval ![]() , where is a sufficiently small positive number.
, where is a sufficiently small positive number.
Points of minimum and maximum called points of extremum, and the values \u200b\u200bof the function corresponding to the points of extremum are called extreme function.

Do not confuse the extremes of the functions with the greatest and smallest function value.

In the first figure, the greatest value of the function on the segment is achieved at the maximum point and equal to the maximum of the function, and on the second figure - the greatest value of the function is achieved at the point x \u003d b, which is not a maximum point.
Sufficient conditions of increasing and descending function.
On the basis of sufficient conditions (signs) of increasing and decrease in the function there are gaps of increasing and descending function.
Here is the formulation of signs of increasing and descending function at the interval:
- if the derivative of the function y \u003d f (x) is positive for any x from the x interval, the function increases with x;
- if the derivative of the function y \u003d f (x) is negative for any x from the x interval, then the function decreases to x.
Thus, to determine the gaps of increasing and decrease of the function need:
Consider an example of the location of the increasing and descending of the function to clarify the algorithm.
Example.
Find gaps of increasing and descending function.
Decision.
In the first step, you need to find the field definition area. In our example, the expression in the denominator should not handle it in zero, therefore.
Go to finding a derivative function: 
To determine the gaps of increasing and descending, the function for sufficient signs solving inequality and on the definition area. We use the generalization of the interval method. The only valid root of the numerator is x \u003d 2, and the denominator refers to zero at x \u003d 0. These points break the definition area on the intervals in which the derived function saves a sign. We note these points on a numeric line. The pluses and minuses conventionally denote the intervals on which the derivative is positive or negative. Arrogors from below schematically show an increase in or decreasing the function at the corresponding interval. 
In this way,  and
and  .
.
At point x \u003d 2 The function is defined and continuous, so it should be added to the increase in the increase in the increase in the decrease. At point x \u003d 0, the function is not defined, so this point does not turn on in the desired intervals.
We present a graph of the function to compare the results obtained.

Answer:
The function increases ![]() , decreases on the interval (0; 2].
, decreases on the interval (0; 2].
Sufficient conditions of extremum function.
To find maxima and minima, you can use any of the three signs of extremum, of course, if the function satisfies their conditions. The most common and convenient is the first one.
The first sufficient extremma condition.
Suppose that the function y \u003d f (x) is differentiated into a neighborhood of the point, and at the very point itself is continuous.
In other words:
The algorithm for finding extremum points on the first sign of the extremum function.
- Find the function definition area.
- We find a derivative function on the definition area.
- Determine the zeros of the numerator, zeros of the denominator of the derivative and point of the definition area in which the derivative does not exist (all listed points are called possible extremum pointspassing through these points, the derivative just can change its sign).
- These points break the field of determining the function to the intervals in which the derivative saves a sign. We determine the signs of the derivative on each of the intervals (for example, by calculating the value of the derivative function at any point of the separate interval).
- We choose the points in which the function is continuous and passing through which, the derivative changes the sign - they are extremum points.
Too many words, consider the best examples of finding extremum points and extremums of the function using the first sufficient condition of the extremum function.
Example.
Find extremmas functions.
Decision.
The field definition area is all set valid numbers, except X \u003d 2.
Find a derivative: 
Zeros of the numerator are points x \u003d -1 and x \u003d 5, the denominator refers to zero at x \u003d 2. We celebrate these points on the numeric axis 
Determine the signs of the derivative on each interval, for this we calculate the value of the derivative in any of the points of each interval, for example, at points x \u003d -2, x \u003d 0, x \u003d 3 and x \u003d 6.
Consequently, on the interval, the derivative is positive (in the figure, put a sign plus over this interval). Similarly 
Therefore, over the second interval, we put minus, over the third - minus, above the fourth - plus.
It remains to choose points in which the function is continuous and its derivative changes the sign. These are the points of extremum.
At point x \u003d -1 The function is continuous and the derivative changes the sign from the plus to minus, therefore, according to the first sign of extremum, x \u003d -1 is a maximum point, it corresponds to the maximum function  .
.
At point x \u003d 5 The function is continuous and the derivative changes the sign from a minus on plus, therefore, x \u003d -1 is a minimum point, it corresponds to a minimum of function  .
.
Graphic illustration.

Answer:
Please note: the first sufficient feature of the extremum does not require differentiability of the function at the very point itself.
Example.
Find Extremum Points and Extreme Functions ![]() .
.
Decision.
The field definition area is all many valid numbers. The function itself can be written as: 
Find a derivative function: 
At point x \u003d 0 The derivative does not exist, since the values \u200b\u200bof one-sided limits when the argument is designed to zero, they do not coincide: 
At the same time, the initial function is continuous at point x \u003d 0 (see section Research function on continuity): 
Find the values \u200b\u200bof the argument at which the derivative turns into zero: 
We note all the points obtained on the numeric direct and determine the sign of the derivative on each of the intervals. To do this, calculate the values \u200b\u200bof the derivative in arbitrary points of each interval, for example, when x \u003d -6, x \u003d -4, x \u003d -1, x \u003d 1, x \u003d 4, x \u003d 6.
I.e, 
Thus, on the first sign of extremum, the points of the minimum are ![]() , maximum points are
, maximum points are ![]() .
.
Calculate the corresponding minima function 
Calculate the corresponding features of the function 
Graphic illustration.

Answer:
 .
.
The second sign of the extremum function.
As you can see, this feature of the extremum function requires the existence of a derivative at least to the second order at the point.
Consider a graph of continuous function. y \u003d f (x)shown in the figure.
Meaning function at point x. 1 will be more functions of the function in all neighboring points both on the left and right from x. one . In this case, it is said that the function has at the point x. 1 maximum. At point x. 3 Function obviously also has a maximum. If you consider the point x. 2, then it value the function is less than all adjacent values. In this case, it is said that the function has at the point x. 2 minimum. Similar to the point x. 4 .
Function y \u003d f (x) At point x. 0 has maximumif the function value at this point is greater than its values \u200b\u200bat all points of some interval containing the point x. 0, i.e. If there is such a neighborhood point x. 0 that for all x.≠x. 0 , belonging to this neighborhood there is inequality f (x)<f (X. 0 ) .
Function y \u003d f (x)it has minimum At point x. 0 , If there is such a neighborhood point x. 0 , what for all x.≠x. 0, belonging to this neighborhood, there is an inequality f (x)>f (x 0.
Points in which the function reaches a maximum and a minimum is called extremum points, and the values \u200b\u200bof the function at these points are extremes of the function.
We draw attention to the fact that the function defined on the segment can reach a maximum and a minimum only at points enclosed within the segment under consideration.
Mark that if the function has a maximum at a point, this does not mean that at this point the function is of the greatest value in the entire field of definition. In the figure, discussed above, the function at the point x. 1 has a maximum, although there are points in which the values \u200b\u200bof the function is greater than at the point x. 1 . In particular, f.(x. 1) < f.(x. 4) i.e. The minimum function is greater than the maximum. From the definition of the maximum it follows only that this is the greatest value of the function at points, quite close to the maximum point.
Theorem 1. (Necessary condition for the existence of extremum.) If differentiable function y \u003d f (x)has in point x \u003d X. 0 Extremum, its derivative at this point adds to zero.
Evidence. Let for definiteness at the point x. 0 Function has a maximum. Then with sufficiently small increments Δ x. have f (X. 0 + Δ x)
Turning into these inequalities to the limit at Δ x.→ 0 and considering that the derivative f. "(x. 0) exists, and consequently the limit that stands on the left does not depend on how Δ x. → 0, we get: at δ x. → 0 – 0 f "(x. 0) ≥ 0 A with δ x. → 0 + 0 f "(x. 0) ≤ 0. Since f "(x. 0) determines the number, then these two inequalities are jointly only when f "(x. 0) = 0.
The proven theorem argues that the maximum and minimum points can only be among those values \u200b\u200bof the argument in which the derivative turns into zero.
We considered the case when the function in all points of some segment has a derivative. How is the case in cases where the derivative does not exist? Consider examples.
Examples.
- y.=|x.|.
The function does not have a derivative at the point x.\u003d 0 (at this point the graph of the function does not have a certain tangent), but at this point the function has a minimum, since y.(0) \u003d 0, and at all x.≠ 0y. > 0.
- Let be x.< x
0. Then c.< x
0 I. f "(C)\u003e0.
therefore f "(C) (X- X 0)<
0 and therefore
f (x) - f (x 0 )< 0, i.e. f (x)< f(x 0 ).
- Let be x\u003e X. 0. Then c\u003e X. 0 I. f "(C)< 0. So f "(C) (X- X 0)< 0. therefore f (x) - f (x 0 ) <0,т.е.f (x)< f (X. 0 ) .
- Find the field definition area f (x).
- Find the first derivative function f "(x).
- Determine the critical points for this:
- find valid roots equation f "(x)=0;
- find all values x. at which the derivative f "(x) does not exist.
- Determine the sign of the derivative on the left and right of the critical point. Since the derivative mark remains constant between two critical points, it is sufficient to determine the sign of the derivative at some point to the left and at one point to the right of the critical point.
- Calculate the value of the function at extremum points.
- Find all the critical points of the function in the interval ( a, B.) and calculate the functions of the function at these points.
- Calculate the values \u200b\u200bof the function at the ends of the segment when x \u003d a, x \u003d b.
- Of all the values \u200b\u200bobtained, choose the largest and smallest.

The function does not have a derivative when x.\u003d 0, as it turns into infinity when x.\u003d 0. But at this point the function has a maximum.

The function does not have a derivative when x.\u003d 0, since ![]() for x.→ 0. At this point, the function does not have a maximum, no minimum. Really, f (x)\u003d 0 and x.<0f (x)<0, а при x.>0f (x)>0.
for x.→ 0. At this point, the function does not have a maximum, no minimum. Really, f (x)\u003d 0 and x.<0f (x)<0, а при x.>0f (x)>0.

Thus, from the above examples and the formulated theorem it can be seen that the function may have an extremum only in two cases: 1) at points where the derivative exists and is zero; 2) At point where the derivative does not exist.
However, if at some point x. 0 We know that f "(x 0 ) \u003d 0, then it is impossible to conclude that at the point x. 0 Function has an extremum.
for example. ![]() .
.
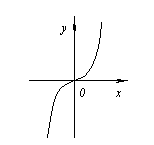
But point x.\u003d 0 is not an extremum point, since to the left of this point, the function value is located below the axis OX.and on the right above.
The values \u200b\u200bof the argument from the function of determining the function, in which the derived function appeals to zero or does not exist, are called critical points.
Of all the above, it follows that the points of extremum functions are among critical points, and, however, not every critical point is an extremum point. Therefore, to find an extremum function, you need to find all the critical points of the function, and then each of these points to explore separately at a maximum and a minimum. For this serves as the following theorem.
Theorem 2. (A sufficient condition for the existence of extremum.) Let the function continuous on some interval containing a critical point x. 0, and differentiable at all points of this interval (except perhaps the point itself x. 0). If when moving from left to right through this point, the derivative changes the sign from the plus to minus, then at the point x. = x. 0 Function has a maximum. If during the transition through x. 0 From left to right, the derivative changes a sign from a minus on plus, the function has at least a minimum.
Thus, if
Evidence. Suppose first that when moving through x. 0 The derivative changes the sign from the plus to minus, i.e. at all x.close to the point x. 0 f "(x)\u003e0 for x.< x 0 , f "(x)< 0 for x\u003e X. 0. Apply Lagrange theorem to the difference f (x) - f (x 0 ) \u003d F "(C) (X- X 0) where c. Lies between x. and x. 0 .
Thus, for all values x. fairly close to k. x. 0 f (x)< f (X. 0 ) . Which means that at the point x. 0 Function has a maximum.
Similarly, the second part of the minimum theorem is proved.
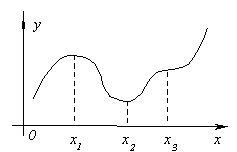
We illustrate the meaning of this theorem in the picture. Let be f "(x 1 ) \u003d 0 and for any xfairly close to k. x. 1, inequalities are performed
f "(x)< 0 as x.< x 1 , f "(x)\u003e0 as x\u003e X. 1 .
Then to the left of the point x. 1 function increases, and on the right decreases, therefore, when x. = x. 1 The function passes from increasing to descending, that is, it has a maximum.
Similarly, you can consider points x. 2 I. x. 3 .

Schematically, all of the above can be depicted in the picture:
Rule of research function y \u003d f (x) to extremum
Examples. Explore functions at least and maximum.
The greatest and smallest values \u200b\u200bof the function on the segment
Great The meaning of the function on the segment is called the largest of all its values \u200b\u200bon this segment, and the smallest - The smallest of all its values.
Consider a function y \u003d f (x) Continuous on segment [ a, B.]. As you know, this function reaches its greatest and smallest values, or on the border of the segment or inside it. If the greatest or smallest value of the function is achieved in the inner point of the segment, this value is a maximum or minimum function, that is, it is achieved at critical points.
Thus, we get the following the rule of finding the greatest and smallest values \u200b\u200bof the function on the segment [ a, B.] :
Turn to the graph of the function y \u003d x 3 - 3x 2. Consider the neighborhood of the point x \u003d 0, i.e. Some interval containing this point. It is logical that there is such a neighborhood of the point x \u003d 0, which the most value of the function y \u003d x 3 - 3x 2 in this neighborhood takes at point x \u003d 0. For example, on the interval (-1; 1) the greatest value 0, the function takes At point x \u003d 0. The point x \u003d 0 is called the point of the maximum of this function.
Similarly, the point x \u003d 2 is called a point of a minimum function x 3 - 3x 2, since at this point the function value is not greater than its value at another point of the neighborhood of the point x \u003d 2, for example, the surroundings (1.5; 2.5).
Thus, the maximum point F (x) is called point x 0, if there is a neighborhood of the point X 0 - such that the inequality F (x) ≤ f (x 0) is performed for all x from this neighborhood.
For example, the point x 0 \u003d 0 is the point of the maximum function f (x) \u003d 1 - x 2, since f (0) \u003d 1 and the inequality F (x) ≤ 1 is true at all values.
The point of the minimum function f (x) is called point X 0, if there is such a neighborhood of the point x 0, which is carried out inequality f (x) ≥ f (x 0) for all x from this neighborhood.
For example, the point x 0 \u003d 2 is the point of the minimum function f (x) \u003d 3 + (x - 2) 2, since f (2) \u003d 3 and f (x) ≥ 3 for all x.
Points of extremum are the points of a minimum and a maximum point.
We turn to the function f (x), which is determined in some neighborhood of the point x 0 and has a derivative at this point.
If x 0 is the extremum point of the differentiable function f (x), then f "(x 0) \u003d 0. This statement is called the farm theorem.
The farm theorem has a visual geometric meaning: at the extremum point is tangent parallel to the abscissa axis and therefore its angular coefficient
F "(x 0) is zero.
For example, the function f (x) \u003d 1 - 3x 2 has at the point x 0 \u003d 0 maximum, its derivative F "(x) \u003d -2x, f" (0) \u003d 0.
The function f (x) \u003d (x - 2) 2 + 3 has a minimum at point x 0 \u003d 2, f "(x) \u003d 2 (x - 2), f" (2) \u003d 0.
Note that if f "(x 0) \u003d 0, this is not enough to assert that x 0 is a necessarily point of extremum function F (x).
For example, if f (x) \u003d x 3, then f "(0) \u003d 0. However, the point of the extremum point x \u003d 0 is not, since the function X 3 increases on the entire numeric axis.
So, the points of extremum differentiable function must be searched only among the roots of the equation
f "(x) \u003d 0, but the root of this equation is not always a point of extremum.
Stationary points are called points in which the derivative function is zero.
Thus, in order for the point x 0 to be an extremum point, it is necessary that it is a stationary point.
Consider sufficient conditions that the stationary point is an extremum point, i.e. Conditions when performing a stationary point is a point of a minimum or maximum function.
If the derivative of the leftmost point is positive, and the right is negative, i.e. The derivative changes the "+" sign on the "-" sign when switching through this point, this stationary point is a maximum point.
Indeed, in this case, the left of the stationary point is the function increases, and to the right - decrease, i.e. This point is a maximum point.
If the derivative changes the sign "-" on the "+" sign when moving through a stationary point, then this stationary point is a minimum point.
If the derivative does not change when switching through a stationary point, i.e. On the left and right of the stationary point, the derivative is positive or negative, then this point is not an extremum point.
Consider one of the tasks. Find the points of the extremum function f (x) \u003d x 4 - 4x 3.
Decision.
1) Find a derivative: F "(x) \u003d 4x 3 - 12x 2 \u003d 4x 2 (x - 3).
2) We will find stationary points: 4x 2 (x - 3) \u003d 0, x 1 \u003d 0, x 2 \u003d 3.
3) the interval method establishes that the derivative F "(x) \u003d 4x 2 (x - 3) is positive at x\u003e 3, negative at x< 0 и при 0 < х < 3.
4) Since when switching through the point x 1 \u003d 0, the derivative mark does not change, then this point is not an extremum point.
5) The derivative changes the sign "-" on the "+" sign when switching through the point x 2 \u003d 3. Therefore, x 2 \u003d 3 is a minimum point.
the site, with full or partial copying of the material reference to the original source is required.