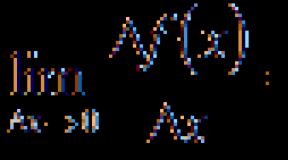Največja vrednost v intervalu. Največje in najmanjše vrednosti funkcije na odseku. Naloge za iskanje največjih in najmanjših vrednosti količin
Preučevanje funkcij in njihovih urnikov je tema, ki ji je v učnem načrtu srednje šole namenjena posebna pozornost. Nekateri temelji matematične analize - diferenciacija - so vključeni v raven profila matematičnega izpita. Nekateri šolarji imajo težave s to temo, saj zamenjajo grafe funkcije in izpeljanke ter pozabijo tudi na algoritme. Ta članek bo obravnaval glavne vrste nalog in načine njihovega reševanja.
Kakšen je pomen funkcije?
Matematična funkcija je posebna enačba. Vzpostavi razmerje med števili. Funkcija je odvisna od vrednosti argumenta.
Vrednost funkcije se izračuna po navedeni formuli. Če želite to narediti, v to formulo namesto x zamenjajte kateri koli argument, ki ustreza obsegu sprejemljivih vrednosti, in izvedite potrebne matematične operacije. Katera vrsta?
Kako lahko z grafom funkcije poiščete najmanjšo vrednost funkcije?
Grafični prikaz odvisnosti funkcije od argumenta se imenuje graf funkcije. Zgrajena je na ravnini z določenim odsekom enote, kjer je vrednost spremenljivke ali argumenta narisana vzdolž vodoravne osi abscis, vrednost funkcije, ki ji ustreza, pa vzdolž osi navpične ordinate.
Večja kot je vrednost argumenta, bolj desno leži na grafikonu. In višja kot je vrednost same funkcije, višja je točka.
Kaj to pomeni? Najmanjša vrednost funkcije bo točka, ki leži pod vsem na grafikonu. Če ga želite najti na segmentu grafa, potrebujete:
1) Poiščite in označite konce tega segmenta.
2) Vizualno določite, katera točka na tem odseku je najnižja.
3) V odgovor zapišite njegovo številčno vrednost, ki jo lahko določite s projiciranjem točke na ordinatno os.
na izpeljani ploskvi. Kje iskati?
Vendar pri reševanju problemov včasih graf ni podan v funkciji, temveč v njeni izpeljavi. Da bi se izognili nenamerni neumni napaki, je bolje natančno prebrati pogoje, saj je odvisno od tega, kje iskati ekstremne točke.

Torej, izpeljanka je trenutna hitrost povečanja funkcije. V skladu z geometrijsko definicijo izpeljanka ustreza naklonu tangente, ki je vlečena neposredno na določeno točko.
Znano je, da je v ekstremnih točkah tangenta vzporedna z osjo Ox. To pomeni, da je njen naklon 0.
Iz tega lahko sklepamo, da na ekstremnih točkah derivat leži na osi abscise ali izgine. Toda poleg tega funkcija na teh točkah spremeni smer. To pomeni, da se po obdobju povečanja začne zmanjševati in se izvedeni finančni instrument v skladu s tem spreminja iz pozitivnega v negativnega. Ali obratno.
Če se izpeljanka iz pozitivne spremeni v negativno, je to največja točka. Če iz negativnega postane pozitiven - minimalna točka.
Pomembno: če je v nalogi treba navesti točko minimuma ali maksimuma, potem v odgovor zapišite ustrezno vrednost vzdolž osi abscise. Če pa želite najti vrednost funkcije, morate v funkcijo najprej nadomestiti ustrezno vrednost argumenta in jo izračunati.
Kako najti ekstremne točke s pomočjo izpeljanke?
Obravnavani primeri se v glavnem nanašajo na postavko številka 7 izpita, ki vključuje delo z grafom derivata ali antiderivata. Toda naloga 12 USE - najti najmanjšo vrednost funkcije na segmentu (včasih tudi največjo) - se izvede brez risb in zahteva osnovne veščine matematične analize.
Če ga želite izvesti, morate z izpeljavo najti ekstremne točke. Algoritem za njihovo iskanje je naslednji:
- Poiščite izpeljanko funkcije.
- Nastavite na nič.
- Poiščite korenine enačbe.
- Preverite, ali so pridobljene točke ekstremne ali prevojne točke.
Če želite to narediti, morate narisati diagram in določiti znake izpeljanke na nastalih intervalih, tako da v izpeljanko nadomestite številke, ki pripadajo odsekom. Če pri reševanju enačbe dobite korenine dvojne množitve, so to prevojne točke.
- Z uporabo izrekov določite, katere točke so najmanjše in katere največje.
Izračun najmanjše vrednosti funkcije z uporabo izpeljanke
Po končanih vseh teh akcijah pa bomo našli vrednosti najmanjše in največje točke vzdolž osi abscis. Kako pa najti najmanjšo vrednost funkcije na odseku?
Kaj je treba storiti, da bi našli številko, ki ji funkcija ustreza na določeni točki? V to formulo morate nadomestiti vrednost argumenta.
Najmanjša in največja točka ustrezata najmanjšim in največjim vrednostim funkcije na odseku. Torej, če želite najti vrednost funkcije, morate funkcijo izračunati z uporabo dobljenih vrednosti x.
Pomembno! Če morate v nalogi navesti najmanjšo ali največjo točko, potem v odgovor zapišite ustrezno vrednost vzdolž osi abscise. Če pa morate najti vrednost funkcije, morate v funkcijo najprej nadomestiti ustrezno vrednost argumenta in izvesti potrebne matematične operacije.
Kaj če na tem segmentu ni minimalnih točk?
Kako pa najti najmanjšo vrednost funkcije na odseku, kjer ni ekstremnih točk?
To pomeni, da se funkcija na njem monotono zmanjšuje ali povečuje. Nato je treba vrednost funkcije skrajnih točk tega segmenta nadomestiti. Obstajata dva načina.
1) Po izračunu izpeljanke in intervalov, v katerih je pozitivna ali negativna, zaključite, ali se funkcija zmanjša ali poveča na danem odseku.
V skladu z njimi v funkcijo nadomestite večjo ali manjšo vrednost argumenta.

2) Samo nadomestite obe točki v funkcijo in primerjajte dobljene vrednosti funkcije.
Pri katerih nalogah iskanje izpeljanke ni obvezno
Praviloma morate v opravilih USE še vedno najti izpeljanko. Obstaja le nekaj izjem.
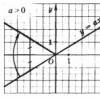
1) Parabola.

Vozlišče parabole najdemo s formulo.
Če< 0, то ветви параболы направлены вниз. И ее вершина является точкой максимума.
Če je a\u003e 0, so veje parabole usmerjene navzgor, vrh pa je najmanjša točka.
Ko ste izračunali točko točke parabole, morate v funkcijo nadomestiti njeno vrednost in izračunati ustrezno vrednost funkcije.
2) Funkcija y \u003d tg x. Ali y \u003d ctg x.
Te funkcije se monotono povečujejo. Zato je večja kot je vrednost argumenta, večja je tudi vrednost same funkcije. Nato si bomo s primeri ogledali, kako najti največjo in najmanjšo vrednost funkcije na segmentu.
Osnovne vrste nalog
Naloga: najvišja ali najnižja vrednost funkcije. Primer na grafikonu.
Na sliki lahko vidite graf izpeljanke funkcije f (x) na intervalu [-6; 6]. Na kateri točki segmenta [-3; 3] f (x) ima najmanjšo vrednost?

Torej, najprej izberite določeni segment. Na njem funkcija enkrat sprejme ničlo in spremeni svoj znak - to je točka ekstrema. Ker izpeljanka iz negativnega postane pozitivna, to pomeni, da je to najmanjša točka funkcije. Ta točka ustreza vrednosti argumenta 2.

Še naprej preučujemo primere. Naloga: poiščite največjo in najmanjšo vrednost funkcije na odseku.
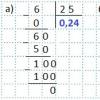
Poiščite najmanjšo vrednost funkcije y \u003d (x - 8) e x-7 na odseku.
1. Vzemimo odvod kompleksne funkcije.
y "(x) \u003d (x - 8) e x-7 \u003d (x - 8)" (e x-7) + (x - 8) (e x-7) "\u003d 1 * (e x-7) + (x - 8) (e x-7) \u003d (1 + x - 8) (e x-7) \u003d (x - 7) (e x-7)
2. Nastalo izpeljanko enačimo z ničlo in rešimo enačbo.
(x - 7) (e x - 7) \u003d 0
x - 7 \u003d 0 ali e x-7 \u003d 0
x \u003d 7; e x-7 ≠ 0, brez korenin
3. V funkcijo nadomestimo vrednost skrajnih točk in izhajajoče korenine enačbe.
y (6) \u003d (6 - 8) e 6-7 \u003d -2e -1
y (7) \u003d (7 - 8) e 7-7 \u003d -1 * e 0 \u003d -1 * 1 \u003d -1
y (8) \u003d (8 - 8) e 8-7 \u003d 0 * e 1 \u003d 0
V tem članku smo torej obravnavali osnovno teorijo o tem, kako najti najmanjšo vrednost funkcije na odseku, ki je potrebna za uspešno reševanje nalog USE v matematiki profila. Tudi elementi matematične analize se uporabljajo pri reševanju nalog iz dela C izpita, vendar očitno predstavljajo drugačno stopnjo kompleksnosti in algoritme za njihove rešitve je težko umestiti v okvir enega gradiva.
Poglejmo, kako raziskati funkcijo z uporabo grafa. Izkazalo se je, da lahko ob pogledu na grafikon ugotovite vse, kar nas zanima, in sicer:
- domena funkcije
- obseg funkcij
- ničle funkcije
- naraščajoče in padajoče intervale
- največ in najmanj točk
- največja in najmanjša vrednost funkcije na odseku.

Pojasnimo terminologijo:
Abscisa je vodoravna koordinata točke.
Odrediti je navpična koordinata.
Os abscise - vodoravna os, ki jo najpogosteje imenujemo os.
Os Y - navpična os ali os.
Prepir je neodvisna spremenljivka, od katere so odvisne vrednosti funkcije. Najpogosteje indicirano.
Z drugimi besedami, sami izberemo, funkcije nadomestimo v formulo in dobimo.
Domena funkcije - nabor tistih (in samo tistih) vrednosti argumenta, za katere funkcija obstaja.
Označuje ga: ali.
Na naši sliki je domena funkcije segment. Na tem segmentu je narisan graf funkcij. Le tukaj ta funkcija obstaja.
Območje funkcij je nabor vrednosti, ki jih sprejme spremenljivka. Na naši sliki je to segment - od najnižje do najvišje vrednosti.
Funkcije ničle - točke, kjer je vrednost funkcije enaka nič, tj. Na naši sliki so to točke in.
Vrednosti funkcije so pozitivne kje . V naši sliki so to vrzeli in.
Vrednosti funkcije so negativne kje . Ta interval (ali interval) imamo od do.
Najpomembnejši koncepti so povečevanje in zmanjševanje funkcije na določenem nizu. Kot niz lahko vzamete segment, interval, združitev intervalov ali celotno številsko črto.
Funkcija povečuje
Z drugimi besedami, več, več, to je graf gre v desno in navzgor.
Funkcija zmanjšuje na množici, če za katero koli in ki pripada množici, neenakost izhaja iz neenakosti
Pri padajoči funkciji večja vrednost ustreza manjši vrednosti. Graf gre desno in dol.
Na naši sliki se funkcija v intervalih povečuje, v intervalih pa zmanjšuje in.
Določimo, kaj je največje in najmanjše točke funkcije.
Največja točka je notranja točka domene definicije, tako da je vrednost funkcije v njej večja kot na vseh točkah, ki so ji dovolj blizu.
Z drugimi besedami, največja točka je taka točka, vrednost funkcije, pri kateri večkot v sosednjih. To je lokalna "gomila" na karti.
Na naši sliki - največja točka.
Najmanjša točka - notranja točka področja definicije, tako da je vrednost funkcije v njej manjša kot na vseh točkah, ki so ji dovolj blizu.
To pomeni, da je minimalna točka taka, da je vrednost funkcije v njej manjša kot v sosednjih. To je lokalna "luknja" na grafikonu.
Na naši sliki - minimalna točka.
Bistvo je meja. To ni notranja točka domene in zato ne ustreza definiciji najvišje točke. Saj na levi strani nima sosedov. Na enak način ne more biti minimalna točka na našem grafikonu.
Skupno se imenujeta največja in najmanjša točka ekstremne točke funkcije... V našem primeru je in.
In kaj storiti, če morate na primer najti minimalna funkcija na segmentu? V tem primeru je odgovor. Ker minimalna funkcija je njegova vrednost na najmanjši točki.
Prav tako je največja naša funkcija. Doseže se v določeni točki.
Lahko rečemo, da so ekstremi funkcije enaki in.
Včasih pri nalogah, ki jih morate najti največje in najmanjše vrednosti funkcije na danem segmentu. Ni nujno, da sovpadajo s skrajnostmi.
V našem primeru najmanjša vrednost funkcije na odseku je enako in sovpada z minimumom funkcije. Toda njegova največja vrednost na tem segmentu je enaka. Dosežemo ga na levem koncu vrstice.
V vsakem primeru so največje in najmanjše vrednosti zvezne funkcije na odseku dosežene bodisi na ekstremnih točkah bodisi na koncih odseka.
Standardni algoritem za reševanje takšnih nalog predpostavlja, da po iskanju ničel funkcije določi znake izpeljanke na intervalih. Nato izračun vrednosti na najdenih točkah maksimuma (ali minimuma) in na meji intervala, odvisno od tega, katero vprašanje je v stanju.
Svetujem vam, da to storite nekoliko drugače. Zakaj? Pisal sem o tem.
Predlagam, da se te naloge rešijo na naslednji način:
1. Poiščite izpeljanko.
2. Poiščite ničle izpeljanke.
3. Ugotovite, kateri izmed njih spadajo v dani interval.
4. Izračunamo vrednosti funkcije na mejah intervala in točk 3. točke.
5. Sklepamo (odgovorimo na zastavljeno vprašanje).
Med reševanjem predstavljenih primerov rešitev kvadratnih enačb ni bila podrobno obravnavana, to bi morali imeti. Morali bi tudi vedeti.
Oglejmo si nekaj primerov:
77422. Poiščite največjo vrednost funkcije y \u003d x 3 –3х + 4 na odseku [–2; 0].
Poiščite ničle izpeljanke:

Navedeno v intervalu pogojev pripada točki х \u003d –1.
Vrednosti funkcije izračunamo v točkah –2, –1 in 0:

Največja vrednost funkcije je 6.
Odgovor: 6
77425. Poiščite najmanjšo vrednost funkcije y \u003d x 3 - 3x 2 + 2 na odseku.
Poiščimo izpeljanko dane funkcije:
Poiščite ničle izpeljanke:
Točka x \u003d 2 pripada intervalu, določenemu v pogoju.
Vrednosti funkcije izračunamo v točkah 1, 2 in 4:

Najmanjša vrednost funkcije je –2.
Odgovor: -2
77426. Poiščite največjo vrednost funkcije y \u003d x 3 - 6x 2 na odseku [–3; 3].
Poiščimo izpeljanko dane funkcije:
Poiščite ničle izpeljanke:
Točka x \u003d 0 pripada intervalu, določenemu v pogoju.
Vrednosti funkcije izračunamo v točkah –3, 0 in 3:

Najmanjša vrednost funkcije je 0.
Odgovor: 0
77429. Poiščite najmanjšo vrednost funkcije y \u003d x 3 - 2x 2 + x +3 na odseku.
Poiščimo izpeljanko dane funkcije:
3x 2 - 4x + 1 \u003d 0
Dobimo korenine: x 1 \u003d 1 x 1 \u003d 1/3.
Intervalu, določenemu v pogoju, pripada samo x \u003d 1.
Poiščimo vrednosti funkcije v točkah 1 in 4:

Ugotovili smo, da je najmanjša vrednost funkcije 3.
Odgovor: 3
77430. Poiščite največjo vrednost funkcije y \u003d x 3 + 2x 2 + x + 3 na odseku [- 4; -one].
Poiščimo izpeljanko dane funkcije:
Poiščite ničle izpeljanke, rešite kvadratno enačbo:
3x 2 + 4x + 1 \u003d 0
Dobili smo korenine:

Interval, naveden v pogoju, pripada korenu x \u003d –1.
Poiščite vrednosti funkcije v točkah –4, –1, –1/3 in 1:

Ugotovili smo, da je največja vrednost funkcije 3.
Odgovor: 3
77433. Poiščite najmanjšo vrednost funkcije y \u003d x 3 - x 2 - 40x +3 na odseku.
Poiščimo izpeljanko dane funkcije:
Poiščite ničle izpeljanke, rešite kvadratno enačbo:
3x 2 - 2x - 40 \u003d 0
Dobili smo korenine:

Interval, naveden v pogoju, pripada korenu x \u003d 4.
Poiščite vrednosti funkcije v točkah 0 in 4:

Ugotovili smo, da je najmanjša vrednost funkcije –109.
Odgovor: –109
Razmislite o metodi za določanje največjih in najmanjših vrednosti funkcij brez izpeljanke. Ta pristop lahko uporabimo, če imate velike težave z opredelitvijo izpeljanke. Načelo je preprosto - vse funkcije števila iz intervala nadomestimo v funkcijo (dejstvo je, da je v vseh takih prototipih odgovor celo število).
77437. Poiščite najmanjšo vrednost funkcije y \u003d 7 + 12x - x 3 na odseku [–2; 2].
Nadomestne točke od –2 do 2: Ogled rešitve
77434. Poiščite največjo vrednost funkcije y \u003d x 3 + 2x 2 - 4x + 4 na odseku [–2; 0].
To je vse. Uspeh vam!
Lep pozdrav, Aleksander Krutitskikh.
P.S: Hvaležen bi bil, če bi nam o spletnem mestu povedali na družbenih omrežjih.
Izjava o težavi 2:
Podana je funkcija, ki je določena in neprekinjena v določenem intervalu. Na tem intervalu je treba najti največjo (najmanjšo) vrednost funkcije.
Teoretične osnove.
Izrek (drugi Weierstrassov izrek):
Če je funkcija definirana in neprekinjena v zaprtem intervalu, potem doseže največje in najnižje vrednosti v tem intervalu.
Funkcija lahko doseže svoje najvišje in najnižje vrednosti bodisi na notranjih točkah intervala bodisi na njegovih mejah. Ponazorimo vse možne možnosti. 
Pojasnilo:
1) Funkcija doseže največjo vrednost na levi meji intervala v točki in najmanjšo vrednost na desni meji intervala v točki.
2) Funkcija doseže največjo vrednost v točki (to je največja točka) in najmanjšo vrednost na desni meji intervala v točki.
3) Funkcija doseže največjo vrednost na levi meji intervala v točki in najmanjšo vrednost v točki (to je najmanjša točka).
4) Funkcija je v intervalu konstantna, tj. doseže najnižjo in največjo vrednost v kateri koli točki intervala, najmanjša in največja vrednost pa sta enaki.
5) Funkcija doseže največjo vrednost v točki in najmanjšo vrednost v točki (kljub temu, da ima funkcija na tem intervalu največjo in najmanjšo vrednost).
6) Funkcija doseže največjo vrednost v točki (to je največja točka) in najmanjšo vrednost v točki (to je najmanjša točka).
Komentar:
"Največja" in "največja vrednost" sta različni stvari. To izhaja iz definicije maksimuma in intuitivnega razumevanja izraza "največja vrednost".
Algoritem za reševanje problema 2.
4) Med dobljenimi vrednostmi izberite največjo (najmanjšo) in zapišite odgovor.
Primer 4:
Določite največjo in najmanjšo vrednost funkcije ![]() na segmentu.
na segmentu.
Sklep:
1) Poiščite izpeljanko funkcije. ![]()
2) Z reševanjem enačbe poiščite mirujoče točke (in točke, sumljive na ekstrem). Bodite pozorni na točke, na katerih ne obstaja dvostranski končni odvod. 
3) Izračunajte vrednosti funkcije na mirujočih točkah in na mejah intervala.
4) Med dobljenimi vrednostmi izberite največjo (najmanjšo) in zapišite odgovor.
Funkcija na tem segmentu doseže največjo vrednost v točki s koordinatami.
Funkcija na tem segmentu doseže najmanjšo vrednost v točki s koordinatami.
Pravilnost izračunov lahko preverite tako, da si ogledate graf preučevane funkcije. 
Komentar: Funkcija doseže največjo vrednost na najvišji točki in najmanjšo na meji segmenta.
Poseben primer.
Recimo, da želite najti največjo in najmanjšo vrednost neke funkcije na segmentu. Po opravljenem prvem koraku algoritma, tj. pri izračunu izpeljanke postane jasno, da ima na primer v celotnem obravnavanem intervalu le negativne vrednosti. Ne pozabite, da če je izpeljanka negativna, se funkcija zmanjša. Ugotovili smo, da se funkcija zmanjšuje v celotnem segmentu. Ta položaj je prikazan na grafu 1 na začetku članka.
Funkcija se zmanjša na odseku, tj. nima ekstremnih točk. Slika prikazuje, da bo funkcija zajela najmanjšo vrednost na desni meji segmenta in največjo vrednost na levi. če je izpeljanka na odseku povsod pozitivna, potem se funkcija poveča. Najmanjša vrednost je na levi meji segmenta, največja pa na desni.