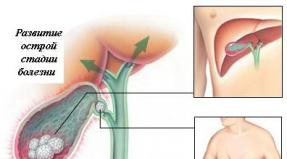
Izpeljano iz eksponenta v stopnjo x. Izpeljanka eksponenta v potenco x Kaj je izpeljanka iz moči x
Pri izpeljavi prve formule tabele bomo nadaljevali z definicijo izpeljave funkcije na točki. Odpelji kam x - katero koli realno število, to je x - poljubno število iz obsega funkcije. Zapišite omejitev razmerja med prirastkom funkcije in prirastkom argumenta pri: ![]()
Upoštevati je treba, da pod mejnim znakom dobimo izraz, ki ni nič negotovosti, deljena z ničlo, saj števec ne vsebuje neskončno majhne vrednosti, in sicer nič. Z drugimi besedami, prirastek konstantne funkcije je vedno nič.
Tako odvod konstantne funkcijeje enako nič na celotnem področju definicije.
Izpeljanka močne funkcije.
Formula za izpeljavo močne funkcije ima obliko ![]() kjer je eksponent str - katero koli realno število.
kjer je eksponent str - katero koli realno število.
Najprej dokažemo formulo za naravni eksponent, to je za p \u003d 1, 2, 3, ...
Uporabili bomo definicijo izpeljanke. Zapišimo mejo razmerja med prirastkom funkcije moči in prirastkom argumenta: 
Za poenostavitev izraza v števcu se obrnemo na Newtonovo binomsko formulo: 
Posledično 
To dokazuje formulo za izpeljavo močne funkcije za naravni eksponent.
Izpeljanka eksponentne funkcije.
Izpeljava izpeljane formule je podana na podlagi definicije:
Prišel v negotovost. Če ga želimo razširiti, uvedemo novo spremenljivko in for. Potem. Pri zadnjem prehodu smo uporabili formulo za prehod na novo osnovo logaritma.
Nadomestimo v prvotni meji: 
Če se spomnimo druge izjemne meje, potem pridemo do formule za odvod eksponentne funkcije: 
Izpeljanka logaritemske funkcije.
Dokažimo formulo za odvod logaritemske funkcije za vse x iz domene definicije in vseh dopustnih vrednosti osnove a logaritem. Po definiciji izpeljanke imamo: 
Kot ste opazili, so bile v dokazu transformacije izvedene z uporabo lastnosti logaritma. Enakost  res na podlagi druge izjemne meje.
res na podlagi druge izjemne meje.
Izpeljanke trigonometričnih funkcij.
Da bi izpeljali formule za izpeljanke trigonometričnih funkcij, se bomo morali spomniti nekaterih formul trigonometrije in prve izjemne meje.
Z definicijo izpeljanke za sinusno funkcijo imamo ![]() .
.
Uporabimo formulo za razliko sinusov: 
Treba se je obrniti na prvo izjemno mejo: 
Tako izpeljanka funkcije greh x tukaj je cos x.
Formula za odvod kosinusa je dokazana na popolnoma enak način. 
Zato izpeljanka funkcije cos x tukaj je –Greh x.
Izpeljava formul tabele izpeljank za tangento in kotangens bo izvedena z uporabo preizkušenih pravil diferenciacije (izpeljanka ulomka). 
Derivati \u200b\u200bhiperboličnih funkcij.
Pravila diferenciacije in formula za izpeljavo eksponentne funkcije iz tabele izpeljank omogočajo izpeljavo formul za odvode hiperboličnega sinusa, kosinusa, tangente in kotangense. 
Izpeljanka inverzne funkcije.
Da se izognemo zmedi v predstavitvi, v podpisu označimo argument funkcije, s katero se opravi diferenciacija, to je izpeljanka funkcije f (x) avtor x.
Zdaj pa formulirajmo pravilo za iskanje izpeljave inverzne funkcije.
Naj funkcije y \u003d f (x) in x \u003d g (y) medsebojno inverzne, določene v intervalih oziroma. Če v točki obstaja končna ne-nična izpeljanka funkcije f (x), potem na točki obstaja končni odvod inverzne funkcije g (y), in ![]() ... V drugem zapisu
... V drugem zapisu ![]() .
.
To pravilo je mogoče preoblikovati za katero koli x iz intervala, potem dobimo  .
.
Preverimo veljavnost teh formul.
Poiščite obratno funkcijo naravnega logaritma ![]() (tukaj y Je funkcija in x- prepir). Reševanje te enačbe za x, smo dobili (tukaj x Je funkcija in y - njen argument). Tj.
(tukaj y Je funkcija in x- prepir). Reševanje te enačbe za x, smo dobili (tukaj x Je funkcija in y - njen argument). Tj. ![]() in medsebojno inverzne funkcije.
in medsebojno inverzne funkcije.
Iz tabele izpeljank to vidimo ![]() in
in ![]() .
.
Poskrbimo, da nas formule za iskanje izpeljank inverzne funkcije vodijo do enakih rezultatov: 
Tu je povzeta tabela za udobje in jasnost pri preučevanju teme.
|
Stalno y \u003d C Močnostna funkcija y \u003d x p (x p) "\u003d p x p - 1 |
Eksponentna funkcija y \u003d a x (a x) "\u003d a x · ln a Zlasti za a \u003d eimamo y \u003d e x (e x) "\u003d e x |
|
Logaritmična funkcija (log a x) "\u003d 1 x ln a Zlasti za a \u003d eimamo y \u003d ln x (ln x) "\u003d 1 x |
Trigonometrične funkcije (sin x) "\u003d cos x (cos x)" \u003d - sin x (t g x) "\u003d 1 cos 2 x (c t g x)" \u003d - 1 sin 2 x |
|
Inverzne trigonometrične funkcije (a r c sin x) "\u003d 1 1 - x 2 (a r c cos x)" \u003d - 1 1 - x 2 (a r c t g x) "\u003d 1 1 + x 2 (a r c c t g x)" \u003d - 1 1 + x 2 |
Hiperbolične funkcije (s h x) "\u003d c h x (c h x)" \u003d s h x (t h x) "\u003d 1 c h 2 x (c t h x)" \u003d - 1 s h 2 x |
Analizirajmo, kako so bile pridobljene formule iz te tabele, ali, z drugimi besedami, dokazali bomo izpeljavo formul za izpeljave za vsako vrsto funkcij.
Izpeljanka konstante
Dokaz 1Da bi izpeljali to formulo, bomo za osnovo vzeli definicijo odvoda funkcije v točki. Uporabimo x 0 \u003d x, kjer x prevzame vrednost katerega koli realnega števila ali, z drugimi besedami, x je poljubno število iz domene funkcije f (x) \u003d C. Zapišimo mejo razmerja med prirastkom funkcije in prirastkom argumenta kot ∆ x → 0:
lim ∆ x → 0 ∆ f (x) ∆ x \u003d lim ∆ x → 0 C - C ∆ x \u003d lim ∆ x → 0 0 ∆ x \u003d 0
Upoštevajte, da izraz 0 ∆ x spada pod mejni znak. Ne gre za negotovost "nič, deljeno z nič", saj števec ne vsebuje neskončno majhne vrednosti, je pa nič. Z drugimi besedami, prirastek konstantne funkcije je vedno nič.
Torej je izpeljanka konstantne funkcije f (x) \u003d C enaka nič v celotni domeni definicije.
Primer 1
Stalne funkcije so podane:
f 1 (x) \u003d 3, f 2 (x) \u003d a, a ∈ R, f 3 (x) \u003d 4. 13 7 22, f 4 (x) \u003d 0, f 5 (x) \u003d - 8 7
Sklep
Opišimo dane pogoje. V prvi funkciji vidimo izpeljanko naravnega števila 3. V naslednjem primeru morate vzeti izpeljanko iz inkje in - katero koli realno število. Tretji primer nam daje izpeljavo iracionalnega števila 4. 13 7 22, četrti je izpeljanka nič (nič je celo število). Končno imamo v petem primeru izpeljavo racionalnega ulomka - 8 7.
Odgovor: izpeljanke danih funkcij so nič za katero koli realno x (v celotni domeni definicije)
f 1 "(x) \u003d (3)" \u003d 0, f 2 "(x) \u003d (a)" \u003d 0, a ∈ R, f 3 "(x) \u003d 4. 13 7 22" \u003d 0, f 4 "(x) \u003d 0" \u003d 0, f 5 "(x) \u003d - 8 7" \u003d 0
Izpeljanka močne funkcije
Preidemo na funkcijo moči in formulo za njen odvod, ki ima obliko: (x p) "\u003d p x p - 1, kjer je eksponent str je katero koli realno število.
Dokaz 2
Tu je dokaz formule, kadar je eksponent naravno število: p \u003d 1, 2, 3, ...
Spet se zanašamo na definicijo izpeljanke. Zapišemo mejo razmerja med prirastkom funkcije moči in prirastkom argumenta:
(x p) "\u003d lim ∆ x → 0 \u003d ∆ (x p) ∆ x \u003d lim ∆ x → 0 (x + ∆ x) p - x p ∆ x
Za poenostavitev izraza v števcu uporabimo Newtonovo binomsko formulo:
(x + ∆ x) p - x p \u003d C p 0 + x p + C p 1 x p - 1 ∆ x + C p 2 x p - 2 ... ... + + C pp - 1 x (∆ x) p - 1 + C pp · (∆ x) p - xp \u003d \u003d C p 1 xp - 1 ∆ x + C p 2 xp - 2 x) 2 +. ... ... + C p p - 1 x (∆ x) p - 1 + C p p (∆ x) p
Tako:
(xp) "\u003d lim ∆ x → 0 ∆ (xp) ∆ x \u003d lim ∆ x → 0 (x + ∆ x) p - xp ∆ x \u003d \u003d lim ∆ x → 0 (C p 1 xp - 1 ∆ x + C p 2 xp - 2 (∆ x) 2 + .. + C pp - 1 x (∆ x) p - 1 + C pp (∆ x) p) ∆ x \u003d \u003d lim ∆ x → 0 (C p 1 xp - 1 + C p 2 xp - 2 ∆ x + .. + C pp - 1 x (∆ x) p - 2 + C pp - 1) \u003d \u003d C p 1 xp - 1 + 0 + 0 + .. + 0 \u003d p!1! (P - 1)! Xp - 1 \u003d p xp - 1
Torej smo dokazali formulo za izpeljavo močne funkcije, kadar je eksponent naravno število.
Dokaz 3
Kot dokaz za primer, ko p -katero koli realno število, ki ni nič, uporabimo logaritemski odvod (tu je treba razumeti razliko od izpeljave logaritemske funkcije). Za popolnejše razumevanje je zaželeno, da preučimo izpeljanko logaritemske funkcije in dodatno razumemo izpeljavo implicitno definirane funkcije in izpeljavo kompleksne funkcije.
Razmislite o dveh primerih: kdaj x pozitivno in kdaj x negativno.
Torej x\u003e 0. Potem: x p\u003e 0. Logaritem enačba y \u003d x p na osnovo e in uporabite lastnost logaritma:
y \u003d x p ln y \u003d ln x p ln y \u003d p ln x
V tej fazi smo dobili implicitno določeno funkcijo. Določimo njegovo izpeljanko:
(ln y) "\u003d (p ln x) 1 y y" \u003d p 1 x ⇒ y "\u003d p y x \u003d p x p x \u003d p x p - 1
Zdaj obravnavamo primer, ko x -negativno število.
Če indikator str je sodo število, potem je za x definirana tudi funkcija moči< 0 , причем является четной: y (x) = - y ((- x) p) " = - p · (- x) p - 1 · (- x) " = = p · (- x) p - 1 = p · x p - 1
Potem x str< 0 и возможно составить доказательство, используя логарифмическую производную.
Če str je liho število, potem je za x definirana tudi funkcija moči< 0 , причем является нечетной: y (x) = - y (- x) = - (- x) p . Тогда x p < 0 , а значит логарифмическую производную задействовать нельзя. В такой ситуации возможно взять за основу доказательства правила дифференцирования и правило нахождения производной сложной функции:
y "(x) \u003d (- (- x) p)" \u003d - ((- x) p) "\u003d - p (- x) p - 1 (- x)" \u003d \u003d p (- x) p - 1 \u003d p xp - 1
Zadnji prehod je mogoč zaradi dejstva, da če str je liho število, torej p - 1 bodisi sodo število bodisi nič (za p \u003d 1), torej za negativno x enakost (- x) p - 1 \u003d x p - 1 je resnična.
Torej smo dokazali formulo za izpeljavo močne funkcije za kateri koli realni p.
2. primer
Funkcije so podane:
f 1 (x) \u003d 1 x 2 3, f 2 (x) \u003d x 2 - 1 4, f 3 (x) \u003d 1 x log 7 12
Določite njihove izpeljanke.
Sklep
Nekatere dane funkcije na podlagi lastnosti stopnje pretvorimo v tabelarno obliko y \u003d x p in nato uporabimo formulo:
f 1 (x) \u003d 1 x 2 3 \u003d x - 2 3 ⇒ f 1 "(x) \u003d - 2 3 x - 2 3 - 1 \u003d - 2 3 x - 5 3 f 2" (x) \u003d x 2 - 1 4 \u003d 2 - 1 4 x 2 - 1 4 - 1 \u003d 2 - 1 4 x 2 - 5 4 f 3 (x) \u003d 1 x log 7 12 \u003d x - log 7 12 ⇒ f 3 "(x) \u003d - log 7 12 x - log 7 12 - 1 \u003d - log 7 12 x - log 7 12 - log 7 7 \u003d - log 7 12 x - log 7 84
Izpeljanka eksponentne funkcije
Dokaz 4Izvedimo formulo za izpeljanko, pri čemer za osnovo vzamemo definicijo:
(ax) "\u003d lim ∆ x → 0 ax + ∆ x - ax ∆ x \u003d lim ∆ x → 0 ax (a ∆ x - 1) ∆ x \u003d ax lim ∆ x → 0 a ∆ x - 1 ∆ x \u003d 0 0
Dobili smo negotovost. Če ga želimo razširiti, zapišemo novo spremenljivko z \u003d a ∆ x - 1 (z → 0 kot ∆ x → 0). V tem primeru je a ∆ x \u003d z + 1 ⇒ ∆ x \u003d log a (z + 1) \u003d ln (z + 1) ln a. Za zadnji prehod se uporablja formula za prehod na novo osnovo logaritma.
Nadomestimo v prvotni meji:
(ax) "\u003d ax lim ∆ x → 0 a ∆ x - 1 ∆ x \u003d ax ln a lim ∆ x → 0 1 1 z ln (z + 1) \u003d \u003d ax ln a lim ∆ x → 0 1 ln (z + 1) 1 z \u003d ax ln a 1 ln lim ∆ x → 0 (z + 1) 1 z
Spomnimo se druge izjemne meje in nato dobimo formulo za odvod eksponentne funkcije:
(a x) "\u003d a x ln a 1 ln lim z → 0 (z + 1) 1 z \u003d a x ln a 1 ln e \u003d a x ln a
3. primer
Podane so okvirne funkcije:
f 1 (x) \u003d 2 3 x, f 2 (x) \u003d 5 3 x, f 3 (x) \u003d 1 (e) x
Poiskati je treba njihove izpeljanke.
Sklep
Za izpeljavo eksponentne funkcije in lastnosti logaritma uporabljamo formulo:
f 1 "(x) \u003d 2 3 x" \u003d 2 3 x · ln 2 3 \u003d 2 3 x · (ln 2 - ln 3) f 2 "(x) \u003d 5 3 x" \u003d 5 3 x · ln 5 1 3 \u003d 1 3 5 3 x ln 5 f 3 "(x) \u003d 1 (e) x" \u003d 1 ex "\u003d 1 ex ln 1 e \u003d 1 ex ln e - 1 \u003d - 1 ex
Izpeljanka logaritemske funkcije
Dokaz 5Predložimo dokaz formule za odvod logaritemske funkcije za katero koli x na področju definicije in morebitne dopustne vrednosti osnove a logaritma. Na podlagi definicije izpeljanke dobimo:
(log ax) "\u003d lim ∆ x → 0 log a (x + ∆ x) - log ax ∆ x \u003d lim ∆ x → 0 log ax + ∆ xx ∆ x \u003d \u003d lim ∆ x → 0 1 ∆ x log a 1 + ∆ xx \u003d lim ∆ x → 0 log a 1 + ∆ xx 1 ∆ x \u003d \u003d lim ∆ x → 0 log a 1 + ∆ xx 1 ∆ x xx \u003d lim ∆ x → 0 1 x log a 1 + ∆ xxx ∆ x \u003d \u003d 1 x log a lim ∆ x → 0 1 + ∆ xxx ∆ x \u003d 1 x log ae \u003d 1 x ln e ln a \u003d 1 x ln a
Iz navedene verige enakovrednosti je razvidno, da so transformacije temeljile na lastnosti logaritma. Enakost lim ∆ x → 0 1 + ∆ x x x ∆ x \u003d e drži po drugi izjemni meji.
4. primer
Podane so logaritemske funkcije:
f 1 (x) \u003d log ln 3 x, f 2 (x) \u003d ln x
Izračunati je treba njihove izpeljanke.
Sklep
Uporabimo izpeljano formulo:
f 1 "(x) \u003d (log ln 3 x)" \u003d 1 x · ln (ln 3); f 2 "(x) \u003d (ln x)" \u003d 1 x · ln e \u003d 1 x
Torej je izpeljanka naravnega logaritma enaka deljeni z x.
Izpeljanke trigonometričnih funkcij
Dokaz 6Za izpeljavo formule za izpeljanko trigonometrične funkcije uporabimo nekaj trigonometričnih formul in prvo izjemno mejo.
Glede na definicijo izpeljanke sinusne funkcije dobimo:
(sin x) "\u003d lim ∆ x → 0 sin (x + ∆ x) - sin x ∆ x
Formula razlike sinusov nam bo omogočila naslednje:
(sin x) "\u003d lim ∆ x → 0 sin (x + ∆ x) - sin x ∆ x \u003d \u003d lim ∆ x → 0 2 sin x + ∆ x - x 2 cos x + ∆ x + x 2 ∆ x \u003d \u003d lim ∆ x → 0 sin ∆ x 2 cos x + ∆ x 2 ∆ x 2 \u003d \u003d cos x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2
Na koncu uporabimo še prvo veliko mejo:
sin "x \u003d cos x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2 \u003d cos x
Torej, izpeljanka funkcije greh x bo cos x.
Dokažimo natančno formulo za odvod kosinusa:
cos "x \u003d lim ∆ x → 0 cos (x + ∆ x) - cos x ∆ x \u003d \u003d lim ∆ x → 0 - 2 sin x + ∆ x - x 2 sin x + ∆ x + x 2 ∆ x \u003d \u003d - lim ∆ x → 0 sin ∆ x 2 sin x + ∆ x 2 ∆ x 2 \u003d \u003d - sin x + 0 2 lim ∆ x → 0 sin ∆ x 2 ∆ x 2 \u003d - sin x
Tisti. izpeljanka funkcije cos x bo - greh x.
Formule za izpeljanke tangente in kotangente izpeljemo na podlagi pravil diferenciacije:
tg "x \u003d sin x cos x" \u003d sin "x cos x - sin x cos" x cos 2 x \u003d \u003d cos x cos x - sin x (- sin x) cos 2 x \u003d sin 2 x + cos 2 x cos 2 x \u003d 1 cos 2 xctg "x \u003d cos x sin x" \u003d cos "x sin x - cos x sin" x sin 2 x \u003d \u003d - sin x sin x - cos x cos x sin 2 x \u003d - sin 2 x + cos 2 x sin 2 x \u003d - 1 sin 2 x
Izpeljanke inverznih trigonometričnih funkcij
Poglavje o izpeljavi inverznih funkcij ponuja izčrpne informacije o dokazovanju formul za odvode inverznega sinusa, inverznega kosinusa, arktangensa in inverznega kotangensa, zato gradiva tukaj ne bomo podvajali.
Derivati \u200b\u200bhiperboličnih funkcij
Dokaz 7Izpeljava formul za derivate hiperboličnega sinusa, kosinusa, tangente in kotangense se izvede z uporabo pravila diferenciacije in formule za derivat eksponentne funkcije:
sh "x \u003d ex - e - x 2" \u003d 1 2 ex "- e - x" \u003d \u003d 1 2 ex - - e - x \u003d ex + e - x 2 \u003d chxch "x \u003d ex + e - x 2" \u003d 1 2 ex "+ e - x" \u003d \u003d 1 2 ex + - e - x \u003d ex - e - x 2 \u003d shxth "x \u003d shxchx" \u003d sh "x chx - shx ch" xch 2 x \u003d ch 2 x - sh 2 xch 2 x \u003d 1 ch 2 xcth "x \u003d chxshx" \u003d ch "x shx - chx sh" xsh 2 x \u003d sh 2 x - ch 2 xsh 2 x \u003d - 1 sh 2 x
Če v besedilu opazite napako, jo izberite in pritisnite Ctrl + Enter
Osnovni pojmi
Preden preučimo vprašanje izpeljave eksponenta v moči $ x $, se spomnimo definicij
- funkcije;
- omejitev zaporedja;
- izpeljanka;
- razstavljavci.
To je potrebno za jasno razumevanje izpeljave eksponenta v moči $ x $.
Opredelitev 1
Funkcija je razmerje med dvema spremenljivkama.
Vzemimo $ y \u003d f (x) $, kjer sta $ x $ in $ y $ spremenljivki. Tu se $ x $ imenuje argument, $ y $ pa funkcija. Argument je lahko poljubnih vrednosti. Spremenljivka $ y $ pa se spreminja v skladu z določenim zakonom, odvisno od argumenta. To pomeni, da je argument $ x $ neodvisna spremenljivka, funkcija $ y $ pa odvisna spremenljivka. Vsaka vrednost $ x $ ima eno vrednost, $ y $.
Če je vsako naravno število $ n \u003d 1, 2, 3, ... $ po nekem zakonu povezano s številom $ x_n $, potem pravijo, da je določeno zaporedje števil $ $_1, x_2, ..., x_n $ . V nasprotnem primeru je takšno zaporedje zapisano kot $ \\ (x_n \\) $. Vsa števila $ x_n $ se imenujejo člani ali elementi zaporedja.
Opredelitev 2
Končna ali neskončna točka številske črte se imenuje meja zaporedja. Omejitev je zapisana na naslednji način: $ \\ lim x_n \u003d \\ lim \\ limit_ (n \\ to \\ infty) x_n \u003d a $. Ta zapis pomeni, da spremenljivka $ x_n $ teži k $ a $ $ x_n \\ do $.
Izpeljanka funkcije $ f $ v točki $ x_0 $ se imenuje naslednja meja:
$ \\ lim \\ limit_ (x \\ do x_0) \\ frac (f (x) - f (x_o)) (x-x_o) $. Označuje se z $ f "(x_0) $.
Število $ e $ je enako naslednji omejitvi:
$ e \u003d \\ lim \\ limite_ (x \\ do \\ infty) (1+ \\ frac (1) (n)) \\ približno 2.718281828459045 ... $
V tej omejitvi je $ n $ naravno ali realno število.
Ker poznamo koncepte mejne, izpeljane in eksponentne, lahko nadaljujemo s preverjanjem formule $ (e ^ x) "\u003d e ^ x $.
Izpeljanka izpeljanke eksponenta v moči $ x $
Imamo $ e ^ x $, kjer je $ x: - \\ infty
$ y "\u003d \\ lim \\ limite _ (\\ Delta x \\ do 0) \\ frac (e ^ (x + \\ Delta x) -e ^ x) (\\ Delta x) $.
Z lastnostjo eksponenta $ e ^ (a + bx) \u003d e ^ a * e ^ b $ lahko pretvorimo števec omejitve:
$ e ^ (x + \\ Delta x) -e ^ x \u003d e ^ x * e ^ (\\ Delta x) -e ^ x \u003d e ^ x (e ^ (\\ Delta x) -1) $.
To pomeni, da je $ y "\u003d \\ lim \\ limit _ (\\ Delta x \\ to 0) \\ frac (e ^ (x + \\ Delta x) -e ^ x) (\\ Delta x) \u003d \\ lim \\ limit _ (\\ Delta x \\ do 0) \\ frac (e ^ x (e ^ (\\ Delta x) -1)) (\\ Delta x) $.
Označimo $ t \u003d e ^ (\\ Delta x) -1 $. Dobimo $ e ^ (\\ Delta x) \u003d t + 1 $ in po lastnosti logaritma se izkaže, da je $ \\ Delta x \u003d ln (t + 1) $.
Ker je eksponent neprekinjen, imamo $ \\ lim \\ limit _ (\\ Delta x \\ to 0) e ^ (\\ Delta x) \u003d e ^ 0 \u003d 1. $ Torej, če je $ \\ Delta x \\ na 0 $, potem $ t \\ do 0 $.
Kot rezultat bomo prikazali preobrazbo:
$ y "\u003d \\ lim \\ limite _ (\\ Delta x \\ do 0) \\ frac (e ^ (\\ Delta x) -1) (\\ Delta x) \u003d e ^ x \\ lim \\ limite_ (t \\ do 0) \\ frac (t) (ln (t + 1)) $.
Označimo $ n \u003d \\ frac (1) (t) $, nato $ t \u003d \\ frac (1) (n) $. Izkazalo se je, da če $ t \\ do 0 $, potem $ n \\ do \\ infty $.
Preoblikujmo svojo mejo:
$ y "\u003d e ^ x \\ lim \\ limite_ (t \\ do 0) \\ frac (t) (ln (t + 1)) \u003d e ^ x \\ lim \\ limite_ (n \\ do \\ infty) \\ frac (1) (n \\ cdot ln (\\ frac (1) (n) +1) ^ n) $.
Po lastnosti logaritma $ b \\ cdot ln c \u003d ln c ^ b $ imamo
$ n \\ cdot ln (\\ frac (1) (n) +1) \u003d ln (\\ frac (1) (n) +1) ^ n \u003d ln (1+ \\ frac (1) (n)) ^ n $ ...
Omejitev se pretvori na naslednji način:
$ y "\u003d e ^ x \\ lim \\ limit_ (n \\ do \\ infty) \\ frac (1) (n \\ cdot ln (\\ frac (1) (n) +1)) \u003d e ^ x \\ lim \\ limite_ ( n \\ do \\ infty) \\ frac (1) (ln (\\ frac (1) (n) +1) ^ n) \u003d e ^ x \\ frac (1) (\\ lim \\ limite_ (n \\ do \\ infty) ln (\\ frac (1) (n) +1) ^ n) $.
Glede na lastnost kontinuitete logaritma in lastnost limitov za zvezno funkcijo: $ \\ lim \\ limit_ (x \\ to x_0) ln (f (x)) \u003d ln (\\ lim \\ limit_f (x)) $, kjer $ f (x) $ ima pozitivno mejo $ \\ lim \\ limit_ (x \\ do x_0) f (x) $. Torej, ker je logaritem neprekinjen in obstaja pozitivna meja $ \\ lim \\ limit_ (n \\ to \\ infty) (\\ frac (1) (n) +1) ^ n $, lahko izpišemo:
$ \\ lim \\ limite_ (n \\ do \\ infty) ln (1+ \\ frac (1) (n)) ^ n \u003d ln \\ lim \\ limite_ (n \\ do \\ infty) ln (1+ \\ frac (1) ( n)) ^ n \u003d ln e \u003d 1 $.
Uporabimo vrednost druge izjemne omejitve $ \\ lim \\ limit_ (n \\ to \\ infty) (1+ \\ frac (1) (n)) ^ n \u003d e $. Dobimo:
$ y "\u003d e ^ x \\ frac (1) (\\ lim \\ limit_ (n \\ to \\ infty) ln (\\ frac (1) (n) +1) ^ n) \u003d e ^ x \\ cdot \\ frac (1 ) (ln e) \u003d e ^ x \\ cdot \\ frac (1) (1) \u003d e ^ x $.
Tako smo izpeljali formulo za izpeljanko eksponenta in lahko trdimo, da je izpeljanka eksponenta na $ x $ potenco enakovredna eksponentu na $ x $ potenco:
Obstajajo tudi drugi načini za pridobitev te formule z uporabo drugih formul in pravil.
Primer 1
Poglejmo si primer iskanja izpeljanke funkcije.
Stanje: Poiščite izpeljanko funkcije $ y \u003d 2 ^ x + 3 ^ x + 10 ^ x + e ^ x $.
Sklep: Za izraze $ 2 ^ x, 3 ^ x $ in $ 10 ^ x $ uporabimo formulo $ (a ^ x) "\u003d a ^ x \\ cdot ln a $. Po izpeljani formuli $ (e ^ x ) "\u003d e ^ x $ četrti izraz $ e ^ x $ se ne spremeni.
Odgovorite: $ y "\u003d 2 ^ x \\ cdot ln 2 + 3 ^ x \\ cdot ln 3 + 10 ^ x \\ cdot ln 10 + e ^ x $.
Tako smo izpeljali formulo $ (e ^ x) "\u003d e ^ x $, pri podajanju definicij osnovnih pojmov pa smo analizirali primer iskanja izpeljanke funkcije z eksponentom kot enim od izrazov.
Številne številke so v antiki dobile svoj obseg in vraževerje. Te dni se jim dodajajo novi miti. Legend o številki pi je veliko, znamenite Fibonaccijeve številke so mu v slavi nekoliko slabše. Toda morda najbolj presenetljivo je število e, brez katerega ne gre sodobna matematika, fizika in celo ekonomija.
Aritmetična vrednost e je približno 2,718. Zakaj ne ravno, ampak približno? Ker je to število iracionalno in transcendentalno, ga ni mogoče izraziti kot ulomek z naravnimi celimi števili ali polinom z racionalnimi koeficienti. Za večino izračunov zadošča navedena natančnost 2,718, čeprav sodobna stopnja računalniške tehnologije omogoča določitev njene vrednosti z natančnostjo več kot bilijona decimalnih mest.
Glavna značilnost števila e je, da je izpeljanka njegove eksponentne funkcije f (x) \u003d e x enaka vrednosti same funkcije e x. Noben drug matematični odnos nima tako nenavadne lastnosti. O tem se pogovorimo malo podrobneje.

Kakšna je meja
Najprej si poglejmo koncept meje. Razmislite o matematičnem izrazu, na primer i \u003d 1 / n. Lahko vidite, da s povečanjem „n ", Vrednost" i "se bo zmanjšala in ko bo" n "težil do neskončnosti (označeno z ∞), bo" i "težil do mejne vrednosti (pogosto imenovane preprosto meja), enake nič. Izraz za mejo (označeno kot lim) za obravnavani primer lahko zapišemo kot lim n → ∞ (1 / n) \u003d 0.
Za različne izraze obstajajo različne omejitve. Ena od teh omejitev, vključena v sovjetske in ruske učbenike kot druga izjemna omejitev, je izraz lim n → ∞ (1 + 1 / n) n. Že v srednjem veku je bilo ugotovljeno, da je meja tega izraza število e.
Prva izjemna meja vključuje izraz lim n → ∞ (Sin n / n) \u003d 1.
Kako najti izpeljanko e x - v tem videu.
Kaj je izpeljanka funkcije
Da bi razkrili koncept izpeljanke, se moramo spomniti, kaj je funkcija v matematiki. Da besedila ne bomo natrpali s kompleksnimi definicijami, se ustavimo na intuitivnem matematičnem konceptu funkcije, ki je sestavljen iz dejstva, da ena ali več količin v njej popolnoma določa vrednost druge količine, če so med seboj povezane. Na primer, v formuli S \u003d π ∙ r 2 površine kroga vrednost polmera r popolnoma in nedvoumno določa površino kroga S.
Funkcije so lahko odvisno od vrste algebrske, trigonometrične, logaritemske itd. V njih so lahko med seboj povezani dva, tri ali več argumentov. Na primer, prevoženo pot S, ki jo je objekt prehodil z enakomerno pospešeno hitrostjo, opišemo s funkcijo S \u003d 0,5 ∙ a ∙ t 2 + V ∙ t, kjer je „t“ čas gibanja, argument „a ”Je pospešek (lahko pozitivna ali negativna vrednost) in" V "začetna hitrost gibanja. Tako je prevožena razdalja odvisna od vrednosti treh argumentov, od katerih sta dva ("a" in "V") konstantna.
Pokažimo s tem primerom osnovni koncept izpeljave funkcije. Označuje hitrost spremembe funkcije na določeni točki. V našem primeru bo to hitrost predmeta v določenem trenutku. Pri konstantnih "a" in "V" je to odvisno samo od časa "t", to pomeni, če govorimo v znanstvenem smislu, moramo izpeljati funkcijo S glede na čas "t".
Ta postopek se imenuje diferenciacija, izvaja se z izračunom meje razmerja med rastjo funkcije in rastjo njenega argumenta za zanemarljivo veliko. Reševanje takšnih problemov za posamezne funkcije je pogosto težko in tukaj ni zajeto. Omeniti velja tudi, da nekatere funkcije na določenih točkah sploh nimajo takšnih omejitev.
V našem primeru je izpeljanka S s časom bo "t" dobil obliko S "\u003d ds / dt \u003d a ∙ t + V, iz česar je razvidno, da se hitrost S" linearno spreminja glede na "t".

Eksponentni derivat
Eksponentna funkcija se imenuje eksponentna funkcija, katere osnova je število e. Običajno je prikazana kot F (x) \u003d e x, kjer je eksponent x spremenljivka. Ta funkcija je popolnoma razločna v celotnem območju realnih števil. Ko x raste, se nenehno povečuje in je vedno večji od nič. Njegova inverzna funkcija je logaritem.

Slavni matematik Taylor je to funkcijo lahko razširil v seriji, imenovani po njem e x \u003d 1 + x / 1! + x 2/2! + x 3/3! +… V območju x od - ∞ do + ∞.
Zakon, ki temelji na tej funkciji, se imenuje eksponentno. Opisuje:
- povečanje sestavljenih bančnih obresti;
- povečanje populacije živali in populacije planeta;
- rigor mortis čas in še veliko več.
Ponovimo še enkrat izjemno lastnost te odvisnosti - vrednost njene izpeljave na kateri koli točki je vedno enaka vrednosti funkcije na tej točki, to je (e x) "\u003d e x.
Tu so izpeljanke za najbolj splošne primere eksponenta:
- (e sekira) "\u003d a ax e sekira;
- (e f (x)) "\u003d f" (x) ∙ e f (x).
Z uporabo teh odvisnosti je enostavno najti izpeljanke za druge posebne vrste te funkcije.
Nekaj \u200b\u200bzanimivosti o številu e
S to številko so povezana imena znanstvenikov, kot so Napier, Otred, Huygens, Bernoulli, Leibniz, Newton, Euler in drugi. Slednji je za to številko dejansko uvedel oznako e in našel tudi prvih 18 števk, pri čemer je za izračun uporabil vrsto e \u003d 1 + 1/1, ki jo je odkril! + 2/2! + 3/3! ...
Številko e najdemo na najbolj nepričakovanih mestih. Na primer, vključen je v enačbo kontaktnega omrežja, ki opisuje povešanje vrvi pod lastno težo, ko so njeni konci pritrjeni na nosilce.
Video
Tema video lekcije je izpeljanka eksponentne funkcije.
Dokaz in izpeljava formul za izpeljanko eksponenta (e v moc x) in eksponentno funkcijo (a v moc x). Primeri izračuna izpeljank e ^ 2x, e ^ 3x in e ^ nx. Izvedene formule višjega reda.
VsebinaPoglej tudi: Eksponentna funkcija - lastnosti, formule, graf
Eksponent, e moči x - lastnosti, formule, graf
Osnovne formule
Izvedek eksponenta je enak samemu eksponentu (izpeljanka e v moči x je enaka e v moči x):
(1)
(e x) ′ \u003d e x.
Izvod eksponentne funkcije z osnovo stopnje a je enak sami funkciji, pomnoženi z naravnim logaritmom a:
(2)
.
Eksponent je eksponentna funkcija, pri kateri je osnova moči enaka številu e, kar je naslednja meja:
.
Tu je lahko naravno ali realno število. Nato izpeljemo formulo (1) za izpeljanko eksponenta.
Izpeljava formule izpeljanega eksponenta
Razmislite o eksponentu, e v moči x:
y \u003d e x.
Ta funkcija je določena za vsakogar. Poiščimo njen odvod glede na spremenljivko x. Po definiciji je izpeljanka naslednja meja:
(3)
.
Ta izraz pretvorimo, da ga zmanjšamo na znane matematične lastnosti in pravila. Za to potrebujemo naslednja dejstva:
IN) Eksponentna lastnost:
(4)
;
B) Lastnost logaritma:
(5)
;
IN) Neprekinjenost logaritma in lastnost omejitev za zvezno funkcijo:
(6)
.
Tu je nekaj funkcij, ki imajo mejo in je ta omejitev pozitivna.
D) Pomen druge izjemne meje:
(7)
.
Ta dejstva uporabljamo do svoje meje (3). Uporabljamo lastnost (4):
;
.
Naredimo zamenjavo. Potem; ...
Zaradi kontinuitete eksponenta
.
Torej, za ,. Kot rezultat dobimo:
.
Naredimo zamenjavo. Potem. Kdaj,. In imamo:
.
Uporabimo lastnost logaritma (5):
... Potem
.
Uporabimo lastnost (6). Ker obstaja pozitivna meja in je logaritem neprekinjen, potem:
.
Tu smo uporabili tudi drugo izjemno mejo (7). Potem
.
Tako smo dobili formulo (1) za odvod eksponentnega.
Izpeljava formule za odvod eksponentne funkcije
Zdaj izpeljemo formulo (2) za odvod eksponentne funkcije z osnovo stopnje a. Verjamemo, da in. Potem eksponentna funkcija
(8)
Določeno za vsakogar.
Pretvorimo formulo (8). Za to bomo uporabili lastnosti eksponentne funkcije in logaritma.
;
.
Torej smo formulo (8) preoblikovali v naslednjo obliko:
.
Izvodi višjega reda e v moči x
Zdaj bomo našli izpeljanke višjih razredov. Najprej poglejmo eksponent:
(14)
.
(1)
.
Vidimo, da je odvod funkcije (14) enak funkciji (14). Z razlikovanjem (1) dobimo izpeljanke drugega in tretjega reda:
;
.
Zato je razvidno, da je tudi izpeljanka n-tega reda enaka prvotni funkciji:
.
Izvodi višjega reda eksponentne funkcije
Zdaj razmislite o eksponentni funkciji z osnovo stopnje a:
.
Našli smo izpeljanko prvega reda:
(15)
.
Z razlikovanjem (15) dobimo izpeljanke drugega in tretjega reda:
;
.
Vidimo, da vsako razlikovanje vodi do množenja prvotne funkcije z. Zato ima izpeljanka n-tega reda naslednjo obliko:
.